Realising Some Useful Functional Circuits Employing the Op-amp Pole:

Now we show how the op-amp pole, which is otherwise parasitic, may be used to advantage in realizing definite types of functional circuits. Assume first the circuits shown in Figure

Supposing the gain of the op-amp to be represented by Eq. a routine analysis of the circuit of Figure (a) yields its input admittance as

Y (s) = ( 1 /R₀) +  A₀ ω_p /s R₀

which represents a parallel-RL admittance with equivalent resistance equal to R_-0 and equivalent inductance L_eq equal to R₀ / A₀ ω_p . Alternatively, a similar analysis of the circuit of the Figure (b) shows

               Z (s) = R₀  +( A₀ ω_p R₀ )/ s

that represents a series-RC impedance with equivalent resistance equal to R₀ and

equivalent capacitance C_eq equal to 1/A₀ ω_p R_p

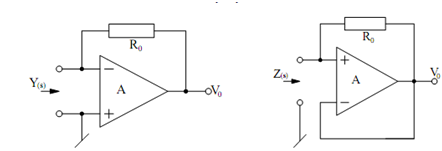
Figure: (a) Simulated Inductor; and (b) Simulated Capacitor

Therefore, one may simulate the effects of an inductance and a capacitance just by using an op- amp and a resistor. These circuits may be utilized to advantage in many situations.