Perfect Bayesian Nash Equilibrium:

Our objective here  is to find a perfect Bayesian Nash equilibrium.  It would of course be useful to give a more precise  statement of Requirement 4 -  one that avoids the  vague  instruction "where possible".  Here we  consider a  three- player game given in the figure below. This game has  one  sub-game  that begins  at player  2's  singleton infonnation set. The unique Nash equilibrium  in this sub-game between players 2 and 3  is (L, R'),  so the unique sub-game perfect Nash equilibrium ofthe entire game is (D,  L,  R').  These  strategies and  the  belief p  =  1  for  player  3  satisfy Requirement  1  through  3. They also  trivially satisfy Requirement  4,  since there is no information set off the equilibrium path, and so constitute a perfect Bayesian Nash  equilibrium.  

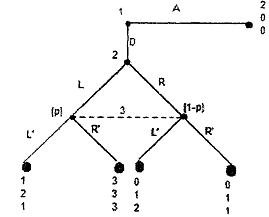
Now  consider the  strategies (A, L, L'),  together with  the belief p = 0. These strategies are a Nash  equilibrium - no  player wants to deviate  unilaterally. These strategies and  belief also satisfy Requirements  1  through 3  -  player 3 has a belief and act optimally given  it, and player 1 and 2 act optimally given the subsequent strategies of the other players. But this Nash equilibrium is not sub-game  perfect, because the  unique Nash  equilibrium of  the  game's  only sub-game is (L, R').  Thus, Requirements 1  through 3 do not guarantee that the player's  strategies are a sub-game perfect ash equilibrium. The problem is that player  3's  belief  (p  = 0)  is inconsistent  with  player  2's  strategy  (L),  but Requirements  1  through  3  impose  no  restrictions  on  3's  belief because  3's information set is not reached  if the game is played according to the specified strategies. Requirement 4,  however, forces player 3's belief to be  determined by  player 2's strategy:  if 2's strategy is L then 3's  belief must be p = 1; if 2's
strategy  is R  then  3's  belief must  be  p = 0. But  if  3's  belief  is  p = 1,  then Requirement 2 forces 3's strategy  to be R';  so the strategies (A, L, L') with p = 0 do not  satisfj Requirements  1  through 4 and therefore do not constitute a perfect Bayesian Nash equilibrium.