Determine the balancing masses and orientation of their radii:
In Figure 5 four masses Wa = 1000 N, Wb = 1500 N, Wc = 1200 N and Wd = 1300 N revolve respectively at radii of ra = 225 mm, rb = 175 mm, rc = 250 mm and rd = 300 mm in planes A, B, C and D. Two planes L & M are chosen to place balancing masses Wl and Wm at a radius of 600 mm. The masses Wb, Wc and Wd are at angles of 45o, 75o and 135o from Wa respectively and distances among planes are : la = 300 mm, lb = 375 mm, lc = 750 mm, ld = 1500 mm, ma = 1800 mm, mb = 875 mm, mc = 500 mm, md = 250 mm. Determine the balancing masses and orientation of their radii from radius of mass Wa.
Solution
See Figure 5. By following Table 1. The distance among planes L and M,
d = ld - md = 1500 - 875 = 825 mm.
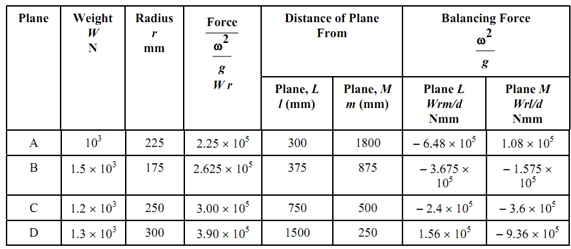
The last two columns illustrate balancing forces for those in planes A and B, etc. Therefore, these forces shall act in opposite direction to Wa, Wb, etc. Four forces in planes L & M shall be equivalent to one force by a single rotating mass. Therefore, two balancing masses - one of each in planes L & M will be achieved.
By balancing forces in L plane are illustrated in Figure 5, along with disturbing forces Wa, Wb, Wc and Wd. To determine resultant of all of the balancing forces we go for their components with horizontal and vertical directions. The relevant angles are illustrated in Figure6.
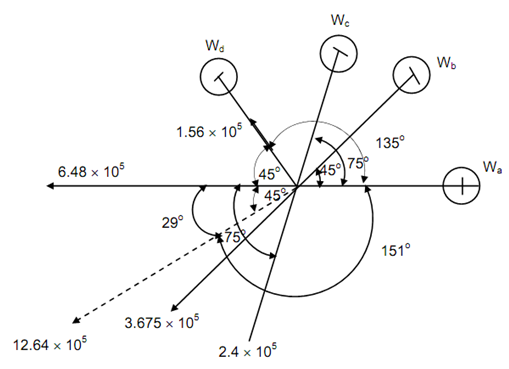
Wr ( H ) = 6.48 × 105 + 3.675 × 105 cos 45 + 2.4 × 105 cos 75 + 1.56 × 105 cos 45
= (6.48 + 2.6 + 0.621 + 1.1) 105
= 10.8 × 105
Wr (V ) = 3.675 × 105 sin 4.5 + 2.4 × 105 sin 75 - 1.56 × 105 sin 45
= (2.6 + 2.32 + 1.1) 105
= 6.02 × 105
W r (Resultant) =
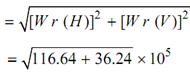
= 12.364 × 105 Nmm
r = 600 mm, W =12.364 × 105 / 600 = 2060.7 N
W = tan -1 W r (V )/ W r (H )
= tan -1 (6.02/ 10.8) = tan -1 0.5574 = 29o
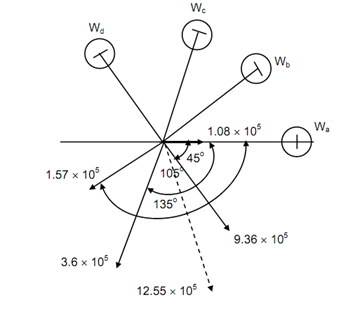
Balancing forces in M plane are illustrated in Figure 7 along with disturbing forces Wa, Wb, Wc and Wd. The resultant is found as above.
Wr (H ) = (1.08 + 1.57 × cos 135 + 3.6 cos 105 + 9.36 cos 45) 105
= (1.08 - 1.11 - 0.93 + 6.62) 105
= 5.66 × 105
Wr (V ) = (1.57 sin 135 + 3.6 sin 105 + 9.36 sin 45) 105
= (1.11 + 3.48 + 6.62) 105
= 11.2 × 105 21
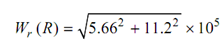
= 12.55 × 105
At r = 600 mm, the balancing mass in M plane shall be
W =12.55 × 105 /600 = 2091 N
It will be placed at angle θ with direction of Wa
θ= tan-1 (11.2/5.66) = tan-1 1.98 = 63.2o
Therefore we see that for balancing the revolving masses in planes A, B, C and D we needs to associate two masses of 2060.7 N and 2091 N, respectively which are among A and B and among C and D.