Determine balancing masses:

A 100 kg mass is fixed to a rotating shaft so that distance of its mass centre from the axis of rotation is equal to 228 mm. Determine balancing masses in following two conditions:

 (i) Two masses - one on left of disturbing mass at a distance of 100 mm and radius of 400 mm, and other on right at a distance of 200 mm and radius of 150 mm.

 (ii) Two masses placed on right of the disturbing mass at distances of 100 and 200 mm and radii of 400 and 200 mm respectively.

The masses are located in the same axial plane.

Solution

For Case (i) see Figure 3.

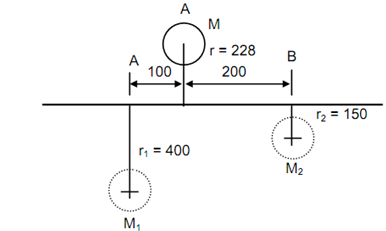
r = 228 mm, l = 100 mm, m = 200 mm, d = l + m = 100 + 200 = 300 mm,

r₁ = 400 mm, r₂ = 150 mm, M = 100 kg, M₁ = ?, M₂ = ?

From Equation (1)

M _r = M₁  r₁  + M ₂  r₂

 100 × 228 = M1 × 400 + M ₂  × 150 (g cancels out)               . . .

 (a) 

 From Equation (6)

M₂   × 150 = 100 × 228 × (100 /300)×(1/19.81)

∴ M ₂  = 9.81 N

(b)   From Equation (7)

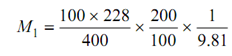
Or M₁  = 9.81 N

(c)    verify with Eq. (i)

22800 = 15200 + 7600

For Case (b) see Figure 4

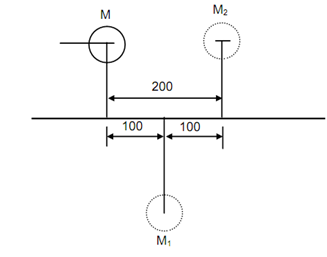
From Eq. (19.6)

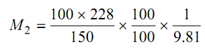
                   (d = 100)

 (iii)

From Equation (7)

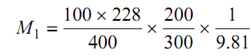
or            M₁  = 9.81 N

 (iv)        From Equation (1)

100 × 228 = 114 × 400 + M ₂ × 150

Or (22800 - 45600)/ 150 × 9.81

W₂  =- 9.81 N                        . . . (v)

 The negative sign shows M₂ is on the other side of M₁.