Balancing of Single Revolving Mass in Two Planes:

The single revolving mass M associated to the shaft at radius r causes the unbalance force and reactions at the support. But, if two masses M₁ at radius r₁ and M₂ at radius r₂ are linked to the shaft, respectively in the similar axial plane then also balancing of force because to rotation of M can be attained. The condition of balance in case as illustrated in Figure 2 shall be

 M ω² r = M₁ ω² r₁ + M ₂ ω² r₂

The bending moments because of the forces and rotating masses will be balanced if

M ω2 r a = M₁  ω r₁ a₁  + M ₂  ω² r₂ a₂

M ω r b = M₁ ω² r₁ b₁ + M ₂ ω² r₂ b₂

a, b, a₁, b₁, a₂ and b₂ are illustrated in Figure 3.

The equations are written again by cancelling out ω² from both sides.

M _r = M₁ r₁ + M ₂  r₂                 ----------- (1)

M _{r a} = M₁ r₁  a₁  + M ₂  r₂  a₂               ----------- (2)

M _{r b} = M₁ r₁ b₁ + M ₂  r₂  b₂              ----------- (3)

Therefore the disturbing force or unbalanced force on the shaft is eliminated. No bending moment is imposed on the shaft and therefore no bending stress. There is no overload at any of bearings A and B.

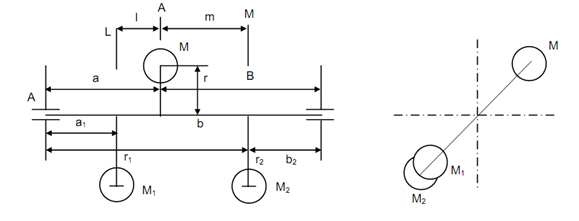
The external balancing along two rotating masses (Figure 2) is resorted to while it is not possible to introduce the balancing mass exactly opposite to disturbing mass in the similar radial plane. This moment shall tend to rock the shaft in the bearings. The balancing masses in the similar axial plane however in two different radial planes might satisfy the conditions of zero force transverse to beam and zero bending moment. The Equation (1), (2) and (3) are such conditions.

If we represents three radial planes for three masses M, M₁ & M₂ as A, L and M, respectively and call distance among A and L as l and that among A and M as m then from Figure 2 it is seen that a = a₁ + l and b = b₂ + m.

Then replacing a through (a₁ + l) and b through (b₂ + m) in Equations (2) and (3), respectively following are achieved.

M  r l = M ₂  r₂  (l + m)

or            M ₂  r₂  = M _r  (l/l + m)            ------------- (4)

and

 M₁  r ₁ = M _r        (m/ l + m)        --------------(5)

 Note down that same results might be obtained if we take moments regarding sections L and M of the shaft. Also note down that Equation (1) implies that reactions at supports are zero. Equations (4) and (5) are more convenient to utilize along with Equation (1) for solving out a problem on external balancing. Again note down that (l + m) is the distance among two radial planes in which balancing masses have been located and these understand that the Equations. (4) And (5) are applicable to a situation as illustrated in Figure 2 but if both L & M are on one side of plane A then also these equations are accurate but one of M₁ and M₂ shall be on the similar side of the shaft like M and (l + m) can be mentioned by d, so that

M ₂  r₂ = M r ( l /d)             --------------(6)

And       M₁ r₁ = M r (m/d)               ----------------- (7)