Use of more than one qualitative variable:

We  can  extend  the  analysis  in. the previous  section  to  handle  more than  one qualitative variable with  ease. Consider once again  the example of salary of school teacher whlch was used  in  the previous  section.  In  this section we assume that the salary of a school teacher to be  dependent not only on  the years of experience and gender of the teacher but also on  the type of education of the teacher. In  the present example  it  is  assumed  that  the type  of  education  has  two categories, convent educated and non-convent educated. Incorporating  the variable type of education of the teacher in  regression model we can write it as:  

In  the above model we  have used two dummy variables one each for the two qualitative explanatory variables 'gender  of the  teacher', and  'type  of education of the teacher'. The base or the benchmark category in the above model is 'nonconvent educated female school teacher'.

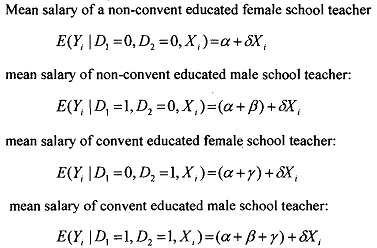
A variety of hypothesis can be tested by  the Ordinary Least Square estimation of the model.  For  example,  we  can  test  for  the  significance  of  the differential intercept terms p or y,  or both P and y  thereby determining which of the possibilities exists without running the regression separately for each combination of gender and type of education.

In  a similar fashion we can extend  the model  to  include more than one quantitative and more than  two qualitative variables. However, we have to always keep in mind that  the number of dummies  for each of  the  qualitative variable should be one less' than the number of categories of that variable.