Nature of dummy variable:

In  regression  analysis the  dependent variable  is  frequently  influenced not  only by variables that  can  be readily quantified on  some well  defined scale (e.g.,  income, output, prices,  costs, weights, etc.), but  also by other variables that are essentially qualitative in  nature (e.g.,  marital status, gender, religion, cute,  ee.).  Shilariy studies in US have  reported that  female college teachers earn  less than their male counterparts. Whatever may be  the  reason  for this  al.,parity,  qwlitative variables  like  gender, institution  of education,  etc.  do  influence the  dependent variable  and should  be included among the independent  variables.  

Since such  qualitative variables  usually  indicate the  presence  or  absence of  some attribute or quality, such as rural or urban, male or female, married or unmarried etc. one can quantify such attributes by  constructing artifical variables  that take value 1 or  0,1 indicating the presence  (or possession)  of  a  particular  attribute  and  0  the absence of it or vice versa. For example, 1 ma)  indicate that the person is a inale and 0 may  indicate that the person  is female; or 1  may  indicate that a person is educated and 0 that he/she is not  educated and  so on. Such variables  which  assume values 0 .and 1 are called Dummy variables.

Like  the  quantitative variables  the  dummy  variable  can  be  used  in  regression analysis very - easily.  In  fact  it may  so happen  that a  regression model may  contain only  dummy  explanatory variables.  Regression models  containing  only  dummy explanatory variables are called  the  analysis  of  variance  (ANOVA) models.  The following model  is an example of ANOVA model

Model is like an  ordinary two variable regression model. The only difference is the use of a qualitative or dummy variable D.  instead of quantitative explanatory variable X.  (From  now on  in  the  present unit we  shall  be  using D  to  denote  the dummy variable). Assuming all  the other  factors such  as age, years of experience, etc. to be constant, the model may enable us to find out whether gender (i.e., being a male or female) makes any difference in  a school teacher's  salary. In  other
words  it  would  enable  us  to  find  out whether  a  male  school  teacher's  salary  is different  from  that of  a  female  school  teacher having the  same qualifications and years of experience.

Assuming the d'igturbance term u,  in  the model satisfies the usual assumptions of  the classical linear regression model  (CLRM),  we  obtain  from  that mean salary of a female school teacher is:

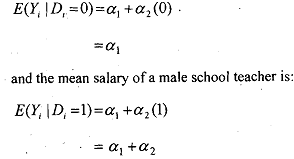
In  the above model the  intercept term α₁ gives the mean  annual salary of a female school teacher while the slope coefficient a2  tells US  how much  the mean  salary of a male  school  teacher  differs  from  that  of  his  female  counterpart with  (α₁ + α₂) reflecting  the mean annual salary of a male school teacher.

1 We  can  also test for  the hypothesis: Is there a discrimination  in  accordance to the gender of an  ihdividual while determining the salary of  school teachers by  running OLS on  the regression equation and finding out on the basis of t-test whether the estimated α₂  is statistically significant or not.