Stresses:

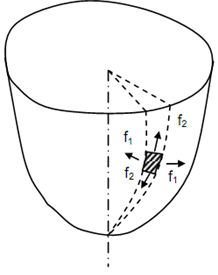
Let a thin walled vessel with two principal radii of curvature r₁ and r₂. Let the thickness of the shell be t and assume it be subjected to an internal pressure of p. The stresses in the two principal directions are f₁ and f₂ working tangential to the middle surface at any specific point as illustrated in Figure

 Figure

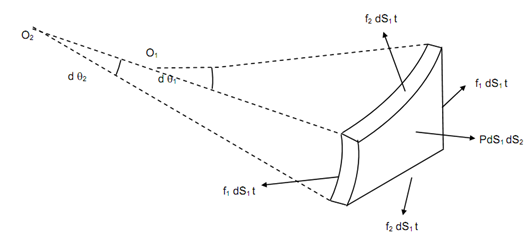
To evaluate the stresses, let the equilibrium of the element illustrated in Figure . Here, f₁ is the circumferential stress & f₂ is the meridional stress. And r₁ is the radius of curvature of the circumferential arc & r₂ the radius of curvature of the meriodional arc.

Figure

For the element, assume

dθ₁ = angle subtended through the circumferential arc at the centre of curvature O₁.

dθ₂ = angle subtended through the meridional arc at the centre of curvature O₂.

ds₁ = length of the circumferential elemental arc.

ds₂ = length of the meridional elemental arc.

The forces working on the surfaces are as shown in Figure. The force f₁ ds₂ t is working in the circumferential direction and f₂ ds₁ t is working in the meridional direction.

The radial force because of the internal pressure on the wall of the element is p ds₁ ds₂. Resolving all of the forces on the elemental part along the normal,

f₁ ds₂ t d θ₁ + f₂ ds₁ t d θ₂  = p ds₁ ds₂

As        d θ₁ =  ds ₁ / r₁         and            d θ₂ =  ds ₂ / r₂

f 1ds₂  t ds₁  / r₁ + f ₂ ds₁ t ds₂ / r₂= p ds₁ ds₂

Therefore, we get    f₁  / r₁ +   f₂ / r₂ =p/ t

The expression gives the general relationship among the circumferential stresses and the meridional stresses along the internal pressure.