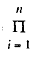The Method of Moment Generating Functions (Approach 3)

One of the easiest method of establish that the distribution of a function Y of random variables x has a known distribution, is to find to mgf of Y and show that it has the same form as the mgf of the known distribution. Obviously, the method is applicable to cases where the mgf exists and the distribution of 'Y is one of the standard probability distribution whose mgf is known. The method is particular useful to find the distribution of the sum of independently distributed random variables.

Let

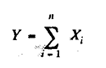
Where X_I, X₂, ..., X_n, are independently distributed variables.

Let the mgf of X_i be .M_i( t ), i = 1,2, ..., n.

The mfg of Y is

M_y (t) = E(e^tY)= E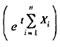

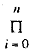   E (e^tXi),since X_i s are independent

Hence

My(t)=