Horizontal equilibrium:

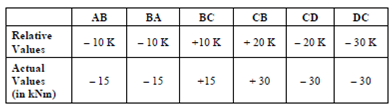
After the above distribution it is clear that the fixed end moments are in the ratios as indicated in the last row, where K is an unknown multiplying factor. To find K we find the support reactions and use the equations of equilibrium.

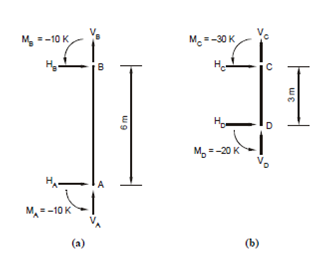
Considering the free body diagram of AB as shown in Figure and taking moments about B, we have

     - H_A × 6 + M_AB + M_BA = 0

-        H_A × 6 - 10 K - 10 K = 0 giving H _A = - 10 K/3

Similarly, considering the free body diagram of CD at Figure 23(b); taking moments about D

or        - H_D • 3 + M_CD + M_DC = 0

or,       - H_D • 3 - 20 K - 30 K = 0 giving H_D  = - 50 K/3

Now considering the horizontal equilibrium of the whole frame (∑ H ≡ 0) We have, H_A + H_D + 30 = 0;

 On substitution - 10 K/3 - 50 K/3 + 30 = 0 giving K = 1.5.

Hence, H _A =-10/3 × 1.5 = - 5 kN, towards left and

H_D = - 50/3× 1.5 = - 25 kN towards right. The negative sign shows that they will be acting in a direction opposite to that shown (i.e. toward left). The moment for the various members will be also multiplied by this factor, K = 1.5, and the final values (in kNm) are shown in kNm is given below :

Figure