Regression approach:

Standard economic theory tells us that each individual will chcose the alternative that maximizes her utility. Let U' be the utility from workingtseeking work and U⁰ be the utility  from not working. Then, the  individual will choose to be  a part of the labor force if her utility from working  is greater than he. utility from not working. In other words, 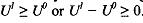  A set of factors, such as age, marital status, gender, education, and work history, gathered in a vector x explain the decision',  so  that

Prob(event j occurs) = Prob(Y_i = j) = G [relevant effects, parameters]

In  our case we have the number of alternatives  indexed by  j = 0, 1; and  the number of individuals  (or obse~ations)  indexed by  i = 1,2,3,.  . .  ..N. Therefore, the probability that the th  individual chooses alternative 1  is given by,  

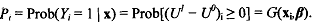
The probability that the th  individual chooses alternative  0 is given by  .

P₁ is commonly called the response probability and 1  -P_i is called the non-response probability. We also have

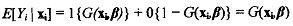
The vector of parameters measures  the impact of changes in x on the probability of labor forc,. participation given the individual's characteristics. For example, we may be  interestea in  the marginal effects of marital status or gender on the probability of labor force participation. The problem at this point is to choose an appropriate model for the right-hand side of the equation, i.e., to choose the appropriate  form of G(x_iβ).