Linear Probability Model:
The linear probability model defines
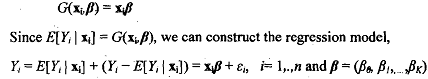
The linear probability model is computationally simple and familiar to all econometrics students. It is equivalent to modeling the choice problem using standard linear regression methodology. However, it has several drawbacks.
1) The right hand side variables are a combination of discrete and continuous variables but the left hand side variable is discrete. We seek to equate "something discrete" to "something continuous". The data plot of the (xi, Yi) observations will plot a series of continoous values against a series of ones and zeros. Fitting a regression line (or plane) by minimizing the squared distance as is done in classical regression analysis does not have any meaningful interpretation here.
2) The choice of values for Y,, i.e., 0 and 1, is arbitrary. This will however, change theb's, which means that thers will have no clear interpretation.
3) As Y, can take only two values, 0 and 1, the disturbance E, also takes only one of two values, for each x,:

Consequently, the behavior of E, can never be approximated by any continuous probability distribution.
4) Standardising E, so that the expectation of e, conditional on the exogenous variables, is zero, as in classical regression analysis implies
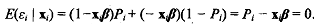
This is turn implies that 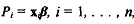 so that the original regression (12.6) is equivalent to
so that the original regression (12.6) is equivalent to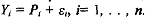 . This gives the disturbance an interpretation as the difference between the binary response variable and the response probability. But, the response probability is usually a continuously varying entity while the disturbance term and the response variable are binary, discrete variables and it does not make sense to equate a discrete variable to the difference between a continuous and a discrete variable.
. This gives the disturbance an interpretation as the difference between the binary response variable and the response probability. But, the response probability is usually a continuously varying entity while the disturbance term and the response variable are binary, discrete variables and it does not make sense to equate a discrete variable to the difference between a continuous and a discrete variable.
The above analysis also implies that the variance of the disturbance is,
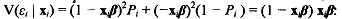
Notice that this variance is a function of both xi and β. In other words, not only is the .variance heteroscedastic but its variance depends on the slope coefficients of the regression .
5) A more serious and fundamental problem is that we cannot constrain xiβ and hence the response probability to the interval [0,1] Consequently, the model produces nonsense probabilities and negative variances. Such predictions are clearly awkward and undesirable. In practice researchers adjust the predicted probabilities to lie within the [0, 1] interval, but such adjustments are ad hoc and the resulting estimator may have no known sampling properties. This is a very serious limitation of the linear model.
For these reasons, the linear model is being less frequently used, except as a basis for comparison to some other more appropriate models.