Sum, Difference, Product and Quotient of Two Functions

If we are given two functions through a common domain, we may form various new functions by applying the four basic operations of subtraction, addition, multiplication and division on them.

(a)        Declare a function δ on D by setting δ (x) = f (x) + g (x). The functions are called upon the sum of the functions f & g, and are indicated by f + g. therefore, (f + g) (x) = f (x) + g (x).

 (b)       Declare a function d on D by setting d (x) = f (x) - g (x). The function d is the function got by subtracting g from f, and is indicated by f - g. Thus, for all x ∈ D, (f - g) (x) = f (x) - g (x).

(c)        Declared a function p on D by setting up p (x) = f (x) g (x). The function p is said the product of the functions f & g, and is indicated by fg. Therefore, for all x ∈ D, (fg) (x) = f (x) g (x).

 (d)       Declared a function q on D by setting q (x) = f (x) . The function p is g (x) provided g (x) ≠ 0 for particular x ∈ D. The function q is called upon the quotient of f by g and is indicated by f/g .Thus

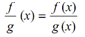
               (g (x) ≠ 0 for any x ∈ D).

Remarks

In case of g (x) = 0 for some x ∈ D, we can let the set, say D′ of all of those values of x for which g (x) ≠ 0 and declared f/g on D' by setting up   

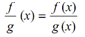                                                          for all x ∈ D′.