Onto Function

Definition 

A function f: X → Y is called to be onto function (or a subjective function) if each member of Y is the image of some of members of X.

Therefore h is not onto function, while g is onto function. Functions that are both one-one and onto (or bijective) are of special significance in mathematics.

Let a function f : X → Y which is both one-one and onto. As f is onto function, each y ∈ Y is the image of some x ∈ X. Also, as f is one-one, y may not be the image of two distinct members of X. Therefore, we discovers that to each y ∈ Y there corresponds a unique x ∈ X such that f (x) = y.

As a result, f sets up one-to-one correspondence among the members of X & Y. this is the one-to-one correspondence among members of X & Y which makes a one-one and onto function so special, as we will soon see.

 Let the function f : N → E stated by f (x) = 2x, where E is the set of even natural numbers. We may see that f is one-one as well as onto. Actually, to each y ∈ E there exists y/2 ∈ N like f (y/2) = y. The correspondence y → y/2 states a function, say g, from E to N like that g (y) = y /2. The function g so defined is called upon as inverse of f. As, to each y ∈ E there corresponds a unique x ∈ N like that f (x) = y just one such function g may be defined equivalent to a given function f. For this cause, g is called upon the inverse of f.

Since you will notice, the function g is also one-one & onto and so this will also have an inverse. You ought to have already guessed that the inverse of g is the function f.

From this conversation we have the following:

If f is one-one & onto function from X to Y, then there presents a unique function g : Y → X like that for each of  y ∈ Y, g (y) = x ⇔ y = f (x). The function g so described is called the inverse of f. Furthermore, if g is inverse of f, then f is the inverse of g, & the two functions f & g are called to be the inverse of each other. Usually the inverse of a function f is mentions by f ^{- 1}.

To discover the inverse of a given function f, we carry on as follows:

Solve out the equation f (x) = y for x. The resultant expression for x (in terms of y) defines as the inverse function.

Therefore, if

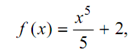
We solve out

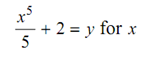
It gives us

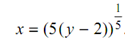
Therefore f ^{- 1} is the function described by f ^-1 ( y) = (5 ( y - 2))1/ 5 .