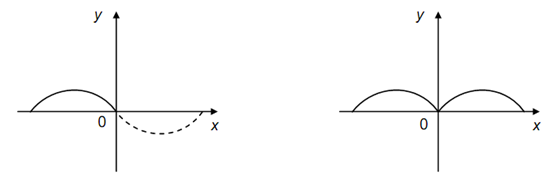Absolute Value Function (or Modulus Function) of a Given Function

Assume f be a function with domain D. The absolute value of function f indicated by | f | & read like mod f is described by setting (| f |) (x) = | f (x) | for all x ∈ D.

As | f (x) | = f (x), if f (x) ≥ 0, therefore | f | have the similar graph for those values of x for which f (x) ≥ 0.

Now, consider those values of x for which f (x) < 0. Here | f (x) | = - f (x). So, the graphs of f & | f | are reflections of each other with Respect to the x-axis for those values of x for which f (x) < 0.

As an instance, consider the graph in fig .The part of the graph below the x-axis, that is, the part for which f (x) < 0 has been indicated as dotted.

To make the graph of | f | we retain the undotted portion in fig as it is, and replace the dotted portion by its reflection with respect to the x-axis.