Intervals on the Real Line

Before we state an interval, understand what is meant by a number line. The real numbers in set R may be put into one-to-one correspondence along the points on a straight line L. In other terms, we shall relate a unique point on L to each of real number and vice-versa.

Let a straight line L .draw a point O on it. The point O will divides the straight line into two parts. We will use the left part of O for representing negative real numbers and the right part of O for representing positive real numbers. We selects a point A on L which is to the right of O. we will represent the number 0 by O & 1 by A. now OA can serve as a unit. To each of positive real number, x we may relate exactly one point P lying to the right of O on L, therefore OP = x units (= x). A negative real number y shall be represented from a point Q lying to the left of O on the straight line L so that OQ = y units (= - y, since y is negative). Thus we find that to each of real number we may relate a point on the line. Also, on the line each of point S represents a unique real number z, like z = OS. Furthermore, if S is to the right of O, z is positive, and it is negative if S is to the left of O.

This representation of real numbers by points on a straight line is frequently very useful. Due to this one-to-one correspondence between real numbers & the points of a straight line, we frequently call a real number "a point of R". Likewise, L is known as a "number line". Note down that the absolute value or the modulus of any of number x is nothing but its just distance from the point O on the number line. In the similar way, x - y mentions the distance between the two numbers x & y .

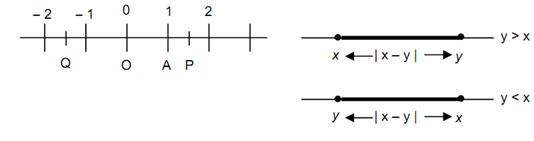
                               (a)                                                              (b) Distance between x and y is | x - y |

Now, consider the set of real numbers which lie among two given real numbers a & b. in fact, there shall be four different sets that satisfying this loose condition. These are following:

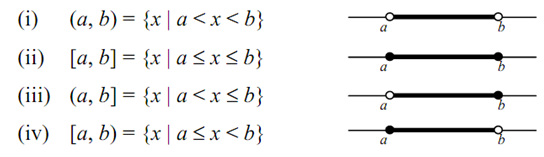
The representation of each sets is given alongside .Each sets is known as an interval, and a & b are known the end points of the interval. The interval (a, b), in which the end points are not included, is called upon an open interval. Note down that in this case we have make a hollow circle around a & b to mentions that they are not included in the graph. The set [a, b] have both its end points is called upon a closed interval. In the representation of this closed interval, we have put thick black dots at a & b to mentions that they are included in the set.

The sets (a, b] & [a, b) are called upon half-open (or half-closed) intervals or semi-open (or semi-closed) intervals, as they have only one end point. This fact is also show in their geometrical representation.

Each of intervals is bounded above by b & bounded below by a. May we represent the set

                                     I = {x : | x - a | < δ}

on the number line? Yes, we can represent. We know that x - a may be thought of as the distance among x & a. It means I is set of all numbers x, whose distance from a is less than δ. therefore, I is the open interval (a - δ, a + δ). Likewise,

                                              I₁ = {x: | x - a | ≤ δ}

is the closed interval [a - δ, a + δ]. Occasionally, we also come across sets as

                                        I₂ = {x: | 0 < | x - a | < δ}

It means if x ∈ I₂, then the distance among x & a is less than δ, but it is not zero. We may also say that the distance among x & a is less than, δ, but x ≠ a.

Therefore,

                           I₂ = (a - δ, a + δ) - {a} = (a - δ, a) ∪ (a, a + δ)

In spite of the four types of intervals listed above, there area a few more types. These are following :

(a, ∞)  = {x | a < x}       (open right ray)

[a, ∞) = {x | a ≤ x}      (closed right ray)

(- ∞, b)  = {x | x < b}   (open left ray)

(- ∞, b]  = {x | x ≤ b}    (closed left ray)

(- ∞, ∞)  = R                  (open interval)

Since you can see easily, none of these sets is bounded. For example, (a, ∞) is bounded below, but it is not bounded above, (- ∞, b) is bounded above, but it is not bounded below. Note down that ∞ does not indicated a real number; it just indicates that an interval extend without limit.

We note down further that if S is any interval (bounded & unbounded) and if c & d are two elements of S then all of numbers lying among c & d are also elements of S.