Graphs of Inverse Functions
There is an interesting relation amongst the graphs of a pair of inverse functions due to which, if the graph of one of them is known, the graph of the other can be determined easily.
Assume f: X → Y is a one-one & onto function, and assume g: Y → X be the inverse of f. A point (p, q) lies on the graph of f ⇔ q = f (p) ⇔ p = g (q) (q, p) lies on the graph of g. The point (p, q) & (q, p) are now reflections of each other with respect to (w. r. t.) the line y = x. so, we can say that the graphs of f & g are reflections of each other w. r. t. the line y = x.
Thus, it follows that, if the graph of one of the functions f & g is given, that of the other can be attained by reflecting it with Respect to the line y = x. As an illustration, the graphs of the functions x3 and y = x1/3 are given in following figure.
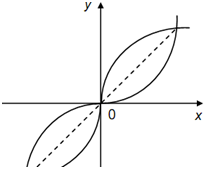
Do you consider that these two functions are inverses of each other? If the sheet of paper on which the graph have been drawn up is folded along the line y = x, the two graphs will accurately coincide.
If a given function is not one-one on its domain, we can select a subset of the domain on which it is one-one & then define its inverse function. For instance, let the function f : x → sin x.
As we know that sin (x + 2π) = sin x, clearly this function is not one-one on R. But if we limit it to the intervals ?- π/2, π/2 ? we discover that it is one-one.
Therefore, if
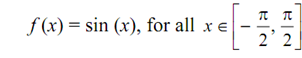
Then we may define
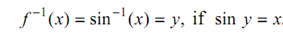
Likewise, we can described cos- 1 & tan- 1 functions as inverse of cosine & tangent functions if we limit the domains to [0, π ] & - π/2 ,π/ 2 respectively.