Example 

For functions f: x → x², ∀ x ∈ R & g : x → 8x + 1, for all x ∈ R, get functions "gof " and "fog".

Solution

"gof " is a function from R to itself, explained by

                                             (gof ) (x) = g (f (x)) = g (x²) = 8x² + 1 for all x ∈ R

"fog " is a function from R to itself, explained by

                                  (fog) (x) = f (g (x)) = f (8x + 1) = (8x + 1)².

Therefore gof & fog are both explained but are different from each other.

The concept of composite functions is utilized not just to combine functions, but also to look upon a given function as build up of two simpler functions. For instance, let the function

                                                  h : x → sin (3x + 7).

We may think of it like the composition (gof) of the functions f : x → 3x + 7, for all x ∈ R & g : u → sin u, for all u ∈ R.

Let us try now to determine the composite functions "fog" & "gof" of the functions:

f : x → 2x + 3, for all x ∈ R, and g : x → (x/2)-(3/2) for all x ∈ R.

Note down that f & g are inverses of each other. Now gof (x) = g (f (x)) = g (2x + 3) = 1/2 (2x + 3) - 3 /2= x.

Likewise,

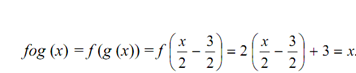
Therefore, we see that gof (x) = x & fog (x) = x are the identity functions on R. What we have viewed here is true for any two functions f & g that are inverses of each of other. Therefore, if f: X → Y & g : Y → X are inverses of each other, then gof & fog are identity functions. As the domain of gof is X & that of fog is Y,

We might write this like:

                                          gof = I_x, fog = I_y

This fact is frequently used to test whether given two functions are inverses of each other or not.