Composition of Functions

Now we will describe a method of joining two functions which is somewhat different from the ones learned so far. Until now, we have assumed functions with the similar domain. We will now consider a pair of functions like that the co-domain of one is the domain of the other.

Consider f : X → Y & g : Y → Z be two functions. We declared a function h : X → Z by setting up h (x) = g (f (x)).

 To get h (x), first we take the f-image f (x) of an element x of X. therefore f (x) ∈Y, that is the domain of g. We then take the g image of f (x), that is, g (f (x)), that is an element of Z. This scheme has been indicated in given figure.

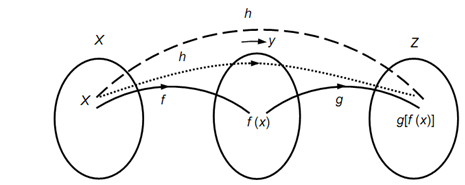
The function h, described above, is known as the composition of f & g and is written like "gof". Note down the order. First we discover the f-image and then its g-image. Attempts to differentiate the composite function gof from the composite function fog that will be declared only while Z is a subset of X.