Absolute Value Function

Another attractive function is the absolute value function (or modulus function) that can be declared by utilizing the concept of the absolute value of a real number like

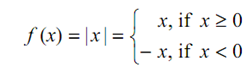
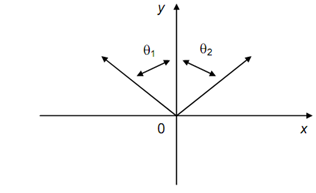
The graph of this function is indicated in given Figure. It consists of two rays; both begin at the origin & making angles π /4 & 3π/4 respectively, along the positive direction of the x-axis.

If a is positive real number other than 1, we described a function

f : R → R by f (x) = a^x where a > 0, a ≠ 1.

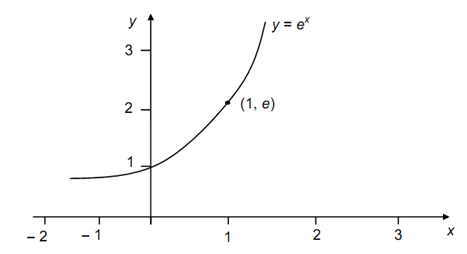
This function is called as the general exponential function. A unique case of this function, where a = e, is frequently found useful. Given fig shows the graph of the function f: R → R such that f (x) = e^x. This function is known as the natural exponential function. Its range is the set R⁺ of positive numbers.