Linear amplifier:

In the following, we carry out a DC analysis of the circuit, to ascertain the range of operation over which it acts as a linear amplifier.

Supposing Q₁ ≅ Q₂ and β₁,₂ >> 1 so that we can assume IE₁, ₂ ≅ I_{C 1, 2,} the application of KVL to the base loop gives

 V_B1 = V_BE1 - V_{BE 2}  + V_{B 2}

Under normal operating condition, according to the Ebers-Moll equations, we have

                                       I_c  ≅ I _s  e ^{(VBE /VT)}       

where I_s stands for the reverse saturation current and V_T = kT/q. Therefore,

V _BE      = V _T ln (   I_C  /I_S)

From Eqs. (34) and (36), we have

V_B1 - V_B2 = V_T ln [  ( I_C1  /I_S2)  /  ( I_C1  /I_S1)

For matched transistors I_S1 = I_S2 so that, we get

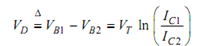
on the other hand, one can write

I_C1 / I_{C 2}= e ^{(VD /VT)}                     

Since,

I_C1 + I_{C 2}  ≅ I _E1 + I _{E 2}  = I _EE  = I₀

Solving Eqs. (39) and (40) for I_C1 and I_C2 we obtain

I₀₁ = I_C1  = I₀ /(1+  e ^{(- VD  / VT )}  )

and

I₀₂ = I_{C 2} =  I₀ /1 + e^{+ (VD/ VT  )}

Figure illustrates a plot of these two equations. From the plot we can note that when V_D

= 0, i.e. V_B1 = V_B2, I_C1 = I_C2 = I_EE /2 which is an expected result due to the supposition of matched devices. Also, for V_D /V_T > 4, I_C1 → I_EE and I_C2 → 0; likewise, for V_D /V_T → 4, I_C1 → 0 and I_C2 → I_EE. Under either of these two conditions, one of the transistors is saturated and the other is cutoff.

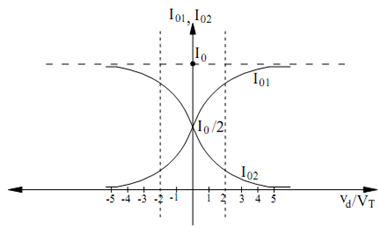
Figure