Differential Mode and Common Mode Gains:

The voltages V₀₁ and V₀₂ are given by

V_01.2  = V_CC  - I_{C1, 2} R_C

where we suppose R_C1 = R_C2 = R_C. Plots of V₀₁ and V₀₂ versus V_D may be made similar to those of Figure In the range - 2 ≤ V_D /V_T  ≤ + 2, V_OD change almost linearity with V_D.

Therefore, in this range the circuit acts as a linear differential amplifier.

To get an analytical expression for V_OD in terms of V_D, we write

                                         V_OD  = V₀₁ - V₀₂

                                            = (I_{C 2}  - I_C1 ) R_C        [from Eq. (43)]

= I _EE R_C [ (1 + e ^{-VD  /VT} )  ^-1  - (1+1 + e^{+ (VD /VT )} ) ^-1  ]  - [From Eqs. (41) and 42)]

The above may be written as :

V _OD      ≅- I _EE  R _C tanh [ V_D/(2V_T )]

obviously, for V_D < - 2 V_T, V₀  ≅ - I _EE R_C and for V_D > 2 V_T ,

V  = (I _EE R_C  /2V _T )V _D

If the sources are taken as v_s1 = v_s/2 and v_s2 = - v_s/2 so that the differential input signal is

v_d = v_s1 - v_s2. This results in small signal base voltages that are equal and opposite, and

Due to symmetry, it follows that the ac current through R_EE must be zero. This, in turn, means v_e = 0; in other terms, the common emitter node may be taken as ac ground. The total circuit thus simplifies to that illustrated in Figure, which is called the differential mode half circuit. That its output voltage is v_od/2 must be obvious from symmetry. From this circuit, the reader may easily find that

A_d   = v_od /v_d =   (v_od/ 2)  / (v_d/2)  = - g_m R_c

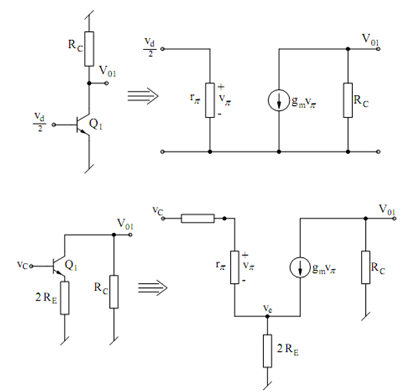
Figure: Equivalent Circuits for the Calculation of Differential Mode and Common Mode Gains