Rotation of Rigid Bodies:

The rotational motion is characterised by the similar angular displacement of all of the points in the rigid body. It follows that the angular velocity, angular displacement, & angular acceleration at a specified point are the same for all the points in the body with reference to the axis of rotation. The trajectory of each of point on the rigid body in rotation must be a circle with its centre on the axis of rotation.

Rotational Motion      

A rigid body is called to be in fixed rotation if there present a fixed strength line in or outside the body such like the points recognize with the body however on that line contain zero velocity and zero acceleration. Rotation can also be mentioned to be about a point if there presents just a fixed point recognize with the body where the velocity and acceleration both vanish. The instance for this is a spinning top regarding the tip and for fixed axis rotation, another instance is a shaft rotating in a fixed journal bearing. This motion is characterised by angular displacement in angular velocity, radians in rad/s & angular acceleration in rad/s². Their relationships can be find out which are as:

Angular displacement = θ rad

Angular velocity =ω = d θ

Angular acceleration, α=d ω / dt = d ² θ /dt ²

Also, Linear velocity,

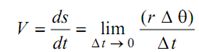
Linear acceleration,

In a pure rolling motion of a sphere or a cylinder, axis or centre moves with rectilinear translation while other points have motion that is combination of rectilinear translation and rotation. The point in contact along stationary surface contains zero velocity. Thus, all of the points in cylinder rotate around this point at a specific instant. The magnitude of the linear velocity will be proportional to the distance from the point of zero velocity.

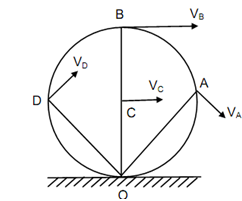
Rolling Motion