Rectilinear Translation:

While particle moves along a straight line, this is said to execute rectilinear translation or motion. We may select x-axis along the line of motion. Thus, from the expression for position vector,

 r = x i              ∴ Δ r = Δ x i

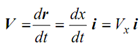                 . . . (1.8)

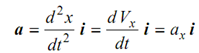. . . (1.9)

If acceleration is constant like in case of motion in gravity field

dV /dt = a                                     . . . (1.10)

 By integrating            V = at + C

Here, C is constant of integration. Its value can be find out if we know initial velocity U

t = 0, V = U

∴          U = a × 0 + C  or  C = U

Thus,    V = at + U                         . . . (1.11)

By further integrating

x = 1 /2at ² + Ut + C

If x = 0 at t = 0

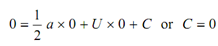
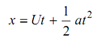. . . (1.12)

From Eqs. (1.11) & (1.12)

V ²  = U ²  + 2aS  . . . (1.13)

here 'S' is distance travelled.

A rigid body is called to be in translation if the linear displacement of each point in the rigid body is similar. This is characterised through the movement of a typical line PQ parallel to itself. In these kinds of motion every point on the body must have similar velocity and similar acceleration at any instant.

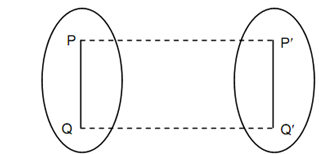
Rectilinear Translation