Curvilinear Motion in a Plane:

A point is called to execute plane motion if it moves in the similar plane. A projectile is very common instance of this motion. A plane may be defined by different sets of coordinate system, for instance cartesian coordinates and polar coordinates etc.

If a plane motion is mentioned by selecting Cartesian coordinates, one term in Equations (1.1), (1.4) and (1.6) will become zero for displacement, velocity and acceleration respectively based on the coordinate axes decided to define the plane of motion. For instance, projectile motion may be defined by x - z plane. The displacement, velocity and acceleration will be expressed as follows :

             r = x i + z k

            V = Vx i + Vz k

and

            a = ax i + az k

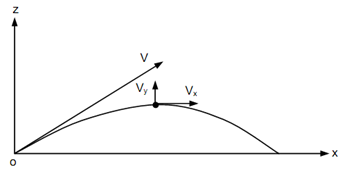
                         Projectile Motion

Consider a point on a circular trajectory in x-y plane.

The position of P at any point can be defined by the x & y coordinates or r & θ coordinates such that

x = r cos θ

y = r sin θ

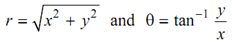
The angular displacement of the instants is Δ θ on a differential time interval Δ t.

Thus, angular velocity

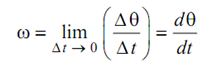
The linear velocity V of the instant is given by following

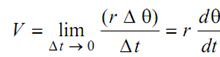
or,        V = r ω

The direction of velocity V is tangential towards the circular path.

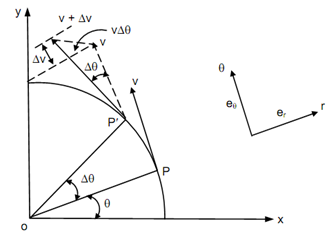
The change in velocity dV may be determined into two components ΔV along direction of θ-axis & V Δ θ along direction of r-axis .Thus, after taking limits the following is attained.

Tangential component of acceleration (a_θ) =dV /dt

Radial component of acceleration (a) = -V d θ / dt

Thus, acceleration a can also be written like following

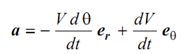
The tangential component is through virtue of change in magnitude of velocity & radial component is through virtue of change in direction.

For a rectilinear motion, the radial component is zero since the radius r of circle is infinite 

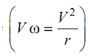
For circular motion at constant speed V, the value of tangential component dV /dt is zero, the point undergoes just change of direction of velocity and this is only subjected to the centripetal acceleration (- ω² r ).

This is sometimes more convenient to define kinematics of a point in terms of path coordinates as illustrated below.

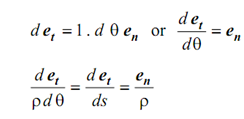
here, ρ is radius of curvature.

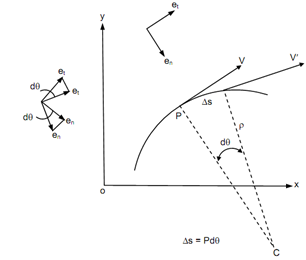
The path coordinates contain following vectors.

e_t - tangential to the path

e_n - directed towards the instantaneous centre of curvature.

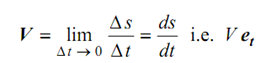
The velocity ought to always be tangential to the path motion of the point

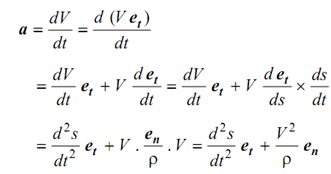
The motion of a rigid body is called to be in plane motion if all of the points in the body stay in the similar parallel planes. A plane motion can be composed of translation & rotation. For instance, rolling of a cylinder without slipping on a curved or flat surface is a plane motion. Translation & rotation may result in a plane motion if the rotation takes place around an axis perpendicular to the plane of motion. Plane motion may also be considered like rotation around a point, called as instantaneous centre of rotation that varies from point to point.

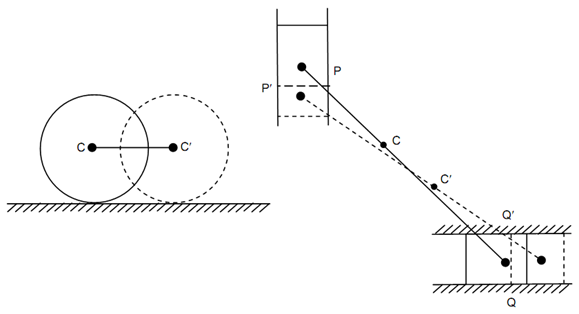
   Combined Motion of Translation and Rotation