Governing Equation for Deflections:

Let us assume a beam represented by its elastic curve as illustrated in Figure , subjected to some arbitrary loading.

Figure

The ACDB is the elastic curve of the beam. The original central line was along to x-axis.

Let us assume a small length CD = ds of the deflected beam, where horizontal distance among C & D is dx.

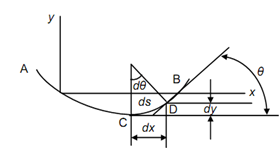
 Figure

The normal drawn to the curve at C and D shall meet at centre of curvature.

Let ds = length of the portion CD,

R = radius of the curvature,

θ = angle made by tangent at D with x-axis, and

dθ = angle construct by radius at C with radius at D.

From above Figure

ds = R d θ

R = ds/ d θ = dx/ d θ              [since ds ≈ dx]

∴          1/ R = d θ   / dx                            ------------- (1)

tan θ= dy/ dx

For small angle, tan θ = θ

 ∴         θ= dy /dx                 ------------- (2)

dy/ dx  is defined as the slope of the curve. In case of deflected beam the curve is the shape of the central line of the beam.

Differentiating the Eq. (9.2), w.r.t., x, we can get

 d θ/ dx = d ² y  / dx²                    -------------- (3)

From Equation. (1) and (3),

1/ R     = d ² y/ dx²                       --------------- (4)

From the theory of pure bending, we know the following,

M / I = E/ R                 ----------------- (5)

 From Eqs. (4) & (5),

M = EI / R = EI (d 2 y /dx2)           --------------- (6)

It is the equation for elastic curve of beam & governing equation for deflections.

Note that y and dy/ dx might be found by integration once & twice, respectively. The condition for integration is that function M = f (x) ought be continuous.