Fracture Criterion
It was in early 1920, when Griffith, by considering a thermodynamic equilibrium of a cracked plate (as shown in Figure 5.5(a)) had shown that the fracture would take place or crack would become unstable, if
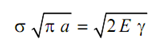
where, E is the modulus of elasticity and σ the surface energy per unit area of the material of the plate. Griffith had not described the result in this form, but he had defined a fracture, stress σf which when reached the fracture would occur. Griffith’s fracture stress was given as,
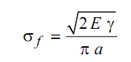----------- (15)
At the time when Griffith’s theory was proposed (i.e. in early 1920s) fracture of material was not recognised as a big problem and hence much importance was not attached to this theory. Now in the light of stress intensity factor of a crack in large plate (Eq. (5)) when W > > a, if one looks at Griffith’s result (Eq. (15)), it is immediately noticed that LHS is the KI value of the crack. The RHS of the equation is nothing but a property of material (product of two properties viz. E and σ ). This prompted Irwin to propose a fracture criterion of a cracked body. “The crack would become unstable, causing body to fracture to its stress intensity factor would assume a critical value”. He further defined that this critical value would be a material property, now known as fracture toughness.
Thus fracture toughness is the property of material that controls the stability of crack in it. As soon as the stress intensity factor of the crack becomes equal to fracture toughness of the material the crack would become unstable and body would fracture. From the definition it is clear that the fracture toughness would have the same units as stress intensity factor itself (it may be noted here that KI corresponds to stress in a defect free smooth specimen and fracture toughness corresponds to strength of material – ultimate tensile strength or yield strength).
Now, one can assume a case in which crack length in a body is continuously increasing due to some reason while a constant gross stress is acting upon it. Since KI is a function of both gross stress and crack length, it will go on increasing as crack length increases even if the load or gross stress remains constant and eventually the fracture would take place as soon as KI become equal to the fracture toughness. This is precisely the reason why the fracture of a cracked body cannot be controlled. In certain region of crack length K may reduce as the crack length increases by a small amount. Such region could be seen as 0 < a/W < 0.2 in Figure 5.7 for 3-point bend specimen with S /W =4 . Similar decrease in KI at constant stress and increasing crack length is also seen prominently in Figure 11 for a single crack on the inside of a thick cylinder. Fracture toughness in Mode I is conventionally denoted by KIC (Read as K-one-C). Similar material properties in Mode II and III are denoted by KIIC and KIIIC.