Fatigue Crack Propagation

It is obvious that for sudden fracture to take place, there must exist a crack of critical length. Such cracks are usually large in length and must be discovered during any non-destructive test. However, crack of such large sizes are not present in the material from the beginning in most of the cases. They initiate during the early part of life of a structure, grow through material even large portion of life and attain macro dimensions which can even be seen visually. These macrocracks then become unstable, causing brittle fracture of the component of the structure. The total time required in this process will, of course, depend upon the design of structure, manufacturing processes through which material passes – particularly those affecting the surface quality, type of loading and environment. Defective design, bad surface finish, fatigue loading and corrosive environment individually or together could cause initiation and propagation of crack. It is most logical to assume that except for fatigue all other factors can be controlled or taken care of by a careful and methodical design process. Fatigue is the only cause that will eventually result in fracture of a machine part or part of structure.

Figure schematically illustrates three different possibilities of crack propagation. If a material in structure carries a defect of size to the order of a mm then fatigue loading soon would cause the crack to extend when KI of the crack will go in increasing until it becomes equal to KIC of the material and fracture occurs. No time is spent in crack initiation because it is not required. Formed or welded parts are liable to have such defects of macro sizes. Metallurgical defects like inclusion may act as microcracks of a few microns length and may propagate further under fatigue loading. Since the size of the crack in such as case is very small, a very large portion of the life would be spent in enlarging of microcrack. Then the crack may assume dimension in the macro range. If the surface of the machine part of structural component is extremely smooth and material is defect free than the crack will initiate on surfaces (it has been explained earlier under “factors affecting fatigue” why cracks initiate on surfaces) and propagate slowly in micro range and then to macro range. In such cases the life spent in fatigue crack propagation is normally 90% of the total life.

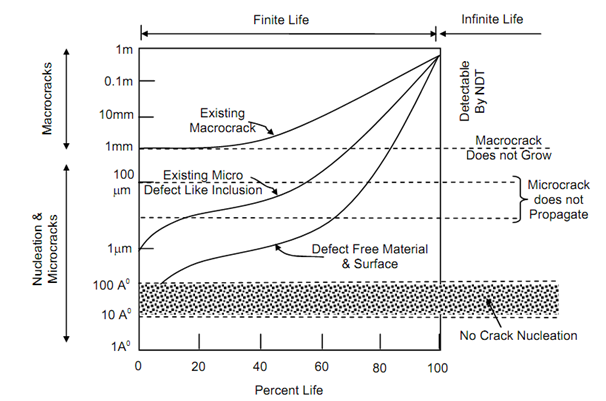
                                  Figure: Schematic Crack Length Variation with Component Life

In such cases when a machine part or structural element has to be designed for infinite life, the stress levels are so chosen that either the crack does not originate (in highly finished surfaces) or if it originated it would not extend to macro size. Not permitting an existing macro crack to grow the critical size will call for a very low stress and will thus make structure uneconomical. It may be noted from Figure that a defect free material with fine surface finish will spend about 90% of its life in crack initiation and microcrack growth. Modern technology and design practices aim at achieving this condition so that either an infinite life may be obtained or a well known crack behaviour during finite life may be predicted. Infinite life, as illustrated in Figure, results if the crack does not nucleate or does not grow into macro region.

Prediction of fatigue life or crack length after certain number of cycles may be done if law of crack propagation is known. Laws of crack propagation during fatigue loading have been experimentally determined for several materials. Such a law is expressed as

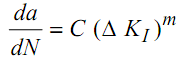
                                            da/ dN = C (ΔK _I )^m                                      ---------- (18)

where  da/ dN is rate of crack propagation in mm/cycle.

Δ K _I is stress intensity factor range or the difference of maximum and minimum stress intensity factors.

                                        Δ K _I = K _{I max}  - K _{I min}

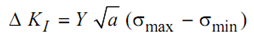
C and m are the constants that depend upon material, environment, frequency, and temperature and stress ratio, i.e. s_max / s_min

 Knowing the law of fatigue crack propagation (i.e. when constants C and m are known), and the length of pre-existing flaw which can be found by an NT test), one can calculate the crack length after a given number of cycles or number of cycles to attain a given crack length. Now applying the knowledge of fracture toughness of material (a property that can be determined experimentally) and relationship between geometry of component and K, one can find out the crack length at which crack would become unstable. Then the number of cycles to reach this crack length may be calculated.

From Eq. (5.5),

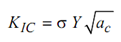
where, ac is critical crack length.

If initial crack length be ai and assuming that ai grows to ac in Nf cycles, then from Eq. (18)

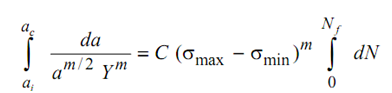                                    ---------- (21)

Integration of LHS of this equation would certainly pose a problem if Y= f (a/W) substituted. Therefore, Eq. (21) usually is to be solved numerically.

If K_I is a simple function of a, as for a large plate (Eq. (22)), then

N_f =      (P ^-m/2 / C )(s_max  - s_min)^{- m} (2/2 - m) (a_c^{(2 - m) / 2} + a_i ^{(2 - m) / 2} )       ---------- (22)

Above description establishes method of finding life of a material component after a finite crack length has been observed. However, the time required for crack initiation and its propagation to macro size is still uncertain. The laws of fatigue crack propagation are established experimentally for different specimens configurations by determining the values of constants C and m.