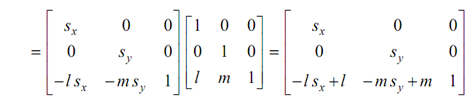Determine scaling matrix:

Determine the transformation that scaled (a) S_x units in x direction (b) S_y units in y direction and Sx and Sy in x and y direction simultaneously. Also determine scaling matrix w. r. t. P (l, m).

Solution

 (a) Scaling transformation applied to point x, y generates the point (ax, y) when scaled in x direction.

Likewise, the point changes to (x, yd) while scaled in y direction by an amount d, so in this case point changes to (x, yb) and while the point is scaled in both of the direction by a and b then the scaling matrix becomes.

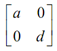
Now, a = s_x and d = s_y. Thus the new point after scaling is

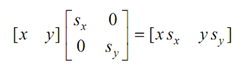
 (b) Now while the scaling is not regarding the origin but about a point P (l, m) then first it ought to be translated to origin, after that scaled and translated back so that

S_{- l , - m}  = T_{l , m}   S_{a , b}  . T_{l , m} 

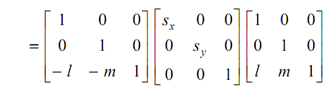
So after concatenation the matrix is following