Find the maximum stress:

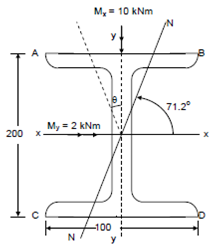
The rolled steel joist shown in Figure is acted upon by a bending moment of 10 kNm acting in the Y-Y plane and 2 kNm acting in the X-X plane. Find the maximum stress in the section and the neutral axis. Given

I_xx = 1696.6 cm⁴ and I_yy = 115.4 cm⁴

Figure

Solution

M_x = 10 kNm = + 10 × 10⁶ Nmm

M_y = - 2 kNm = - 2 × 10⁶ Nmm

As per above sign convention

tan  θ = M_y/M _x = - 2/10= - 0.2

giving θ = 11.3^o (anticlockwise) (the angle made by the resultant moment with the YY axis).

A co-ordinates of the four critical points for which stresses are calculated is given below:

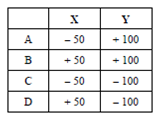
∴ f _A = (M_x/I_xx)y +(M_y/I_yy)x = 10 × 10⁶/1696.6 × 10⁴(+ 100) +(- 2 × 10⁶)/115.4×10⁴ (- 50)

= 58.94 + 86.66 = 145.60 N/mm² (Compressive)

Similarly, f_B =10×10⁶/1696.6×10⁴(+100)+(-2×10⁶)/115.4×10⁴(+50)=58.94 -86.66

= - 27.72 N / mm²(Compressive)

f_C = 10 × 10⁶/1696.6×10⁴ (-100) + (-2×10⁶)/115.4×10⁴(-50)=-58.94+86.66

= - 145.6N/mm²(tensile)

Thus, the maximum compressive stress occurs at the point A, and the maximum tensile stress at D.

An angle α that the neutral axis NN makes with axis XX is given by

tan α =  - I_xx/I_yy tan θ = -1696.6×10⁴/115.4×10⁴ tan(-11.3)

or tan α = 2.9404 ⇒ α = 71^o.2   (anticlockwise).