Auxiliary regressions:

Multicollinearity arises because one or more of the regressors are exact or approximate linear combinations  of the other regressors. One way of finding out which X variable is related to other X variables is to regress each X, on the remaining X variables and compyte the corresponding R₂,  which we designate as R₁  .  Each one of  these regressions is called  an  auxiliary regression; auxiliary to the main regression of Yon X's.  There are subsequently two ways to test for multicollinearity:  

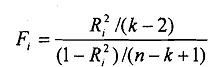
(a) First, we  can  follow   lien's rule of  thumb, which suggests  that multicollinearity  is a troublesome  problem only  if  the R:  obtained  from an auxiliary regression is greater  than the overall R2.

(b) Second,  it can be shown that the variable

follows the F  distribution with degrees of fkeedom k-2  and n-k+ 1. Here, n stands for sample size, k  stands for the number of explanatory variables including the intercept  term, and R₁'  is  the explained variation from the regression of X on the remaining  Xvariables.  If the computed value of F  exceeds the critical values at the chosen level of significance,  then it is  taken to mean that the particularx, is collinear with the otherxs. Conversely,  if  the computed  F  is lower  than the critical value then we say  that it  is  not collinear and we can  retain  it  in  the model.