Deductions for Holes:

Here If two angles placed back to back are not properly tack riveted, each one shall be connected by one leg only and deductions are to be made as in case (a).

Area of the leg of an angle (or tee) shall be taken as follows.

A = t₁ (d - (t₂/2))

where,  t₁ = Thickness of leg,

d = Length of leg (from corner), and

t₂ = Thickness of the other leg.

Example

(Deductions for Holes)

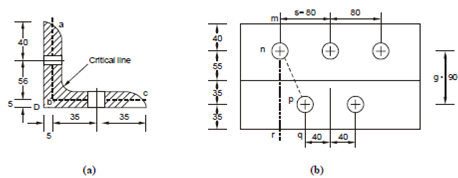
A 100 × 75 × 10 angle is connected by both its legs through 14 mm diameter rivets. Find out the minimum net effective area, if the longer leg is connected by three and shorter leg by two rivets at 80 mm pitch staggered.

Figure

 Solution

The angle with rivet holes is shown in Figure 4(a). The critical line a, b, c is shown dotted. In Figure 4(b), the angle is shown opened up along a-b-c, Edge distance for long leg is 40 mm and for short leg 35 mm.

The gauge length, g is distance between the two rivet hole n and p, i.e.

g = 55 + 35 = 90 mm

Diameter of holes = 14 + 1.5 = 15.5 mm;

Area of 100 × 75 × 10 angle = 1650 mm²

For tearing plane m-n-r there is only one rivet hole

∴ Net effective area = 1650 - 15.5 × 10 = 1495 mm²

For tearing plane m-n-p-q there are two holes and one inclined path

∴ Net effective area = 1650 - 2 × (15.5 × 10) + (40²×10)/4 × 90 = 1351 mm²

Therefore, the smaller value 1351 mm² is the net effective area.