Permissible Deflection and Design for Stiffness
The deflection d1, d2 and d3 are computed from above equations correspondingly. The total deflection of the spindle nose can be ascertained as the sum of three deflections. The design of stiffness can be performed in accordance along with equation. The permissible deflection of the spindle nose dper depends on the machining accuracy needed for the machine tool. Usually, it should be less than one-third of the maximum permissible tolerance on radial run out of the spindle nose. The machining accuracy depends not only on the radial stiffness but as well on its axial and torsional stiffness. The axial displacement of the spindle unit contains the axial deformation of the spindle and the deformation of the spindle thrust bearing. The torsional stiffness of machine tool spindles considerably influences the machining accuracy in metal removal operations like gear and thread cutting in which the feed and primary cutting motions are kinematically related. The torsional deformation of the spindle unit contains the deformation of the spindle and deformation of drive components. As stated earlier, spindles are designed for stiffness, basically radial. Though in heavily loaded spindles the stiffness design must be proved by a strength check against fatigue failure. The strength check requires that
f ≥ f min
Where
f = factor of safety against fatigue failure.
fmin = minimum value of safety factor = 1.3 to 1.5
If spindles are subjected to combined bending and torsion, the factor of safety f is described from the equation,
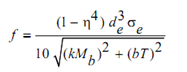
Where
η= di / de Stands for ratio of the internal diameter to the external
di Stands for internal diameter of the spindle, mm
de Stands for external diameter of the spindle, mm
σ e Stands for Endurance limit of the spindle material, N/mm2
Mb Stands for mean value of the bending moment acting on the spindle, N. mm
T Stands for mean value of the torque acting on the spindle, N. mm
k Stands for coefficient that accounts for variation of bending moment and stress concentration.
b Stands for coefficient that accounts for variation of torque and stress concentration.
Coefficient that is denoted by k can be determined from the following expression:
k = U σ (1 + Q)
Where
Uσ = dynamic stress concentration coefficient for normal stresses = 1.7 to 2.0
Q = M ba / M b = ratio of amplitude of the bending moment to its average value.
Coefficient b can be calculated from the subsequent formula:
b = σ e / σy + Uτ Qt
Where
σ y stands for yield stress of the spindle material.
U τ stands for dynamic stress concentration coefficient for shearing stress.
= 1.7 to 2.0
Qt = Ta/T = ratio of amplitude of torque to its average value
The values of Q and Qt usually depend on the machining conditions. For instance, in a super-finishing operation there is virtually no variation of the bending moment and torque, that is Mba = Ta = 0 and Hence Q = Qt = 0.