Deflection of Spindle Axis due to Compliance of Spindle Supports

Let δ_E and δ_G present the displacement of the rear and front support respectively. Owing to compliance support, the spindle deflects are displayed in figure. From similarity of triangles OHH' and OGG'.

Equation

d₂ / m + x = δ_G / x

 ∴ d₂ = (1 + (m / x)) δ_G

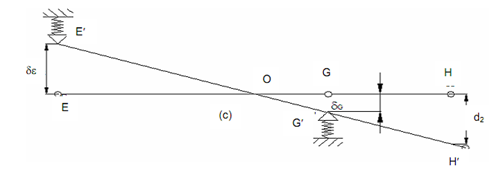
Figure: Deflection of the Spindle due to Compliance of Support

From similarity of triangles OEE' and OGG', we acquire

δ_G / x = δ_E / (a - x)

x = aδ_G / (δ_E + δ_G)

On substituting these values of x in Equation, d₂ changes to,

Equation

d₂ = (1+ (m/a)) δ_G + δ_E (m /a)

Therefore it is clear from above equation that displacement δ_G of the front bearing has greater affect on deflection d₂ of spindle nose than displacement δ_E of the rear bearing.

Displacement  δ_E =   R_E /S_E

And δ_G = R_G / S_G                   

In which R_E and R_G are the support reactions at E and G correspondingly.

S_E and S_G are stiffness at E and G respectively.

At equilibrium,

∑M _E = 0

∴ RG a - F₂ k + M _r - F₁ (m + a) = 0

∴ R _G = F₂ k - M _r + F₁ (m + a) / a

Similarly          ∑ M _G = 0

∴ R_E a - F₂ b - M _r + F₁ m = 0

∴ R_E = (F₂ b + M _r - F₁ m) /a

Equation

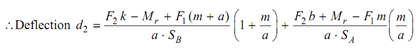
Therefore total deflection d (displayed in below diagram) is obtained as

d = d₁ + d₂

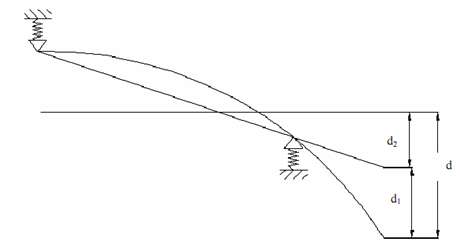
Figure: Total Deflection of Spindle Axis