Determination of Maximum Pressure

It is essential to establish the points of action of the resultant normal forces F₁, F₂ and F₃ on the corresponding faces for calculating the maximum pressure. The distance among the point of action of normal force F₁ on the flat slideway II and the center of the carriage is denoted by x_A . This is shown in diagram. The distance among the force F₂ acting upon the vertical face of flat slideway II and the center of the carriage is indicated by x_B , and the distance between force F₃ acting upon horizontal face of flat slideway II and the center of the carriage is denoted by x_c . For ascertaining x_A , x_B and x_C , we have two equilibrium conditions :

Equation

∑ M_y  = 0

F_x h + F_z x_p  - F₁ x_A  - F₃ x_c  + Rz_Q  = 0

Equation

∑ M_Z  = 0

F_x y_p + F_y x_p  - Ry_Q  - F₂ x_B  +  μF₂ ((l + u)/2) + μF₃l = 0

An additional eq. may be written by assuming that the moment of reactive forces that are F₁ and F₃ about the Y-axis is proportional to the width of the slideway face, that is

Equation

F₁ x_A / F₂ x_c  = v/u

On solving above three Equations we get, the values of x_A , x_B and x_c.

The ratio of  x_A /L, x_B /L and x_c /L computes the shape of the pressure distribution diagram and the maximum pressure on a specific face of the slideway. The process for determining the maximum pressure on flat slideway I is being subjected to the normal force F₁ that is described below. The most common case of pressure distribution along the length of contact L corresponds to a trapezoid as displayed in diagram.

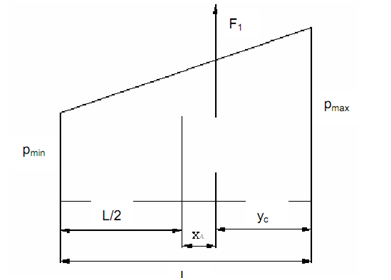
Figure: Trapezoidal Pressure Distribution along Slideway Length

Force F₁ acts at the center of gravity of trapezoid. The distance y_c at the center of gravity from the larger arm of the trapezoid can be ascertained as:

Equation

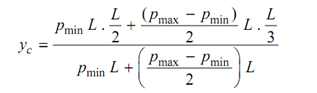
∴ y_c = (L/3) ((p_max + 2 p_min) / (p_max + p_min))

As a result,

Equation

x_A = L/2 - y_c

∴ X_A = L/6 ((p_max + p_min) / (p_max + p_min))

Now x_A / L < 1/6

In this case the pressure distribution diagram presents a trapezoid. This is described with the help of following illustration.

Let (x_A / L) < (1/10)

From equation we attain,

P_max = p_min = 6/10 (p_max + p_min)

P_min = 0.4 / 1.6 p_max

From above equation, it is clear that pmin is a positive, non-zero value. Hence pressure distribution diagram must be a trapezoid.

Equation

∴ p_max   + p_min  = 2 p_av

From Eq. (16), we get,

Equation 23

P_max = P_min = (12x_A / L) P_av

On solving above two Equation

P_max = p_av [1+ (6x_A / L)]