Biaxial Bending:
From your study of Applied Mechanics, you know that for any area there are two mutually perpendicular axes xx and yy about which the moment of inertia of the area Ixx or I yy is either maximum or minimum. These axes are called principal axes. A product of inertia Ixy of the area about the principal axes is zero. That is also known that an axis of symmetry is a principal axis for an area. Hence, in Figures 6(a) the axes xx and yy for the channel and joist sections are principal axes but for angle (Figure 6(c)), the axes parallel to their legs xx and yy are not the principal axes.
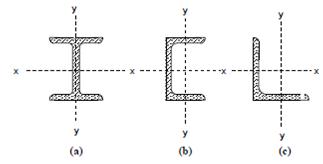
Figure
While the plane of bending lies in the plane of one of the principal axes, the well-known formula f/y = M/I may be applied.
However, there may be instances when bending moments may exist along both the principal axes, or it might act along an axis inclined to the principal axes, so that it has components M cos α and M sin α along the two principal axes. Such cases come under the category of biaxial bending, also known as unsymmetrical bending.