Case of weak electrolytes:

The graph that was described in the above figure is a straight line, for which

Slope = K_a (Λ ^∝) ² = 2.88 × 10^-7 (mol dm^-3) (S m² mol^-1)²

And

K_a = (2.88 × 10^-7/(0.0203)²)mol dm^-3

= 7.0 × 10^-4 mol dm^-3

But, in the case of weak electrolytes, it is not probable to acquire the limiting molar conductivity value, through extrapolation of molar conductivity value to zero concentration as it can be done for strong electrolyte. For weak electrolyte, we can use Kohlarausch's law of independent migration to calculate indirectly value for weak electrolytes as illustrated by the following example:

Λ^∝ (CH₃COOH) = Λ^∝ (CH₃COONa) + Λ^∝ (HCl) -Λ^∝ (NaCl)

Notice that all the terms on the right hand side are for strong electrolytes and are known; thus, we can calculate the value for the weak electrolyte, ethanoic acid (acetic acid) CH₃COOH, as shown below :

The values of molar conductivity at infinite dilution for sodium ethanoate (sodium acetate), hydrochloric acid and sodium chloride are 0.009101, 0.04261 and 0.01264 S m² mol^-1, respectively

Hence, ( Λ^∝ CH₃COOH)   =  [(0.009101 + 0.04261) - 0.01264] S m² mol^-1

=  0.03907 S m² mol^-1

=  390.7 S m² mol^-1

If the molar conductivity of 0.001 mol dm^-3 ethanoic acid is 48.63 S cm2 mol^-1, its degree of dissociation can be calculated using Eq. (6.9), i.e.

α = Λ_m/Λ^∝ = 48.63 S m² mol^-1/390.7 S m² mol^-1

= 0.1245

To calculate dissociation constant of ethanoic acid, substitute that value within Eq. (6.3).

K_a= a²c/ (1 - α) = ((0.1245)² × 0.0001)/1 - 0.1245= 1.77 × 10^-5 mol dm^-3

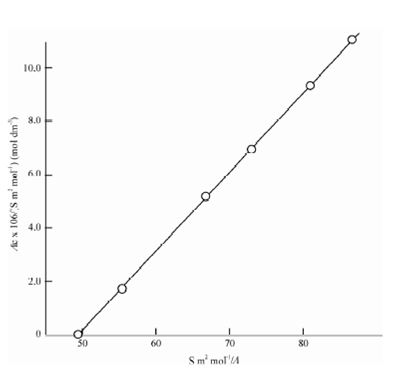
Figure: Plot of Λ_m / c versus 1/ Λ_m