Bar of conical shape:

Now, let us consider the case of a bar whose cross section is varying continuously as display in below figure. A bar of (truncated) conical shape is subjected to an axial force of P. As in the case of stepped bars, here also, we might apply the equation δ = ∑ δ_i = ∑ P_i L_i /A_i E_i, if we recognize that L is sufficiently small and A may be taken as uniform over the length of the small segment. That is, the expression ∑ P_iL_i/A_iE_i now becomes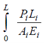

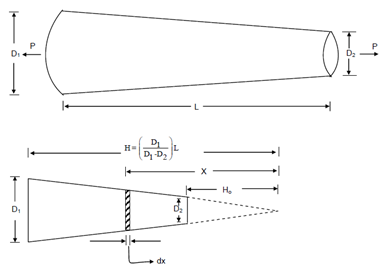
Figure

However, to simplify the expression for A, the origin may be conveniently being shifted to the apex of the produced cone as shown in Figure. Thus,

δ= ∫^H_H0 Pdx/(π/4) (D1x/H)² E

 The integral in above equation may be evaluated for solids having stepped as well as continuous variation in cross section. Stepped bars require no special treatment except that the equilibrium and deformations of each segment may be analysed separately and added wherever necessary. Even a prismatic segment of the bar may have to be considered as two or more members, if external loads are applied at interior points of the segment.