SS Beams with UDL:

Figure illustrated a simply supported beam of span l & loaded by an udl of w per unit length.

Because of symmetry,

R_A  = R_B = wl/ 2

Let a section X-X at a distance x from A,

M = (wl /2)x - w x . (x/2)

= wl x  /2 - w x²/2

Figure

The governing equation for deflection is following:

EI( d ² y/ dx²)  = w l x/2- w x2/2

Integrating the Eq. (28), we can obtain

EI dy/ dx = (w l x2/4) - w x³/6+ C₁

EIy = wl x³ / 12 - w x⁴/24 + C₁ x + C₂

The constants C₁ and C₂ may be found from the boundary conditions. The boundary conditions are following:

at A, x = 0,                    y = 0                                                 ---------------- (1)

at B, x = l,                     y = 0                                                  -------------- (2)

at C,  x = l /2,                 dy / dx = 0                                           ---------------(3)

By applying the BC (1) to Equation (30), C₂ = 0.

By applying the BC (2) to the Equation (30),

0 = wl ⁴ /12 - wl ⁴ /24 + C₁ l  ∴ C1 = wl ³ /24

The slope & deflection equations shall be,

EI (dy/ dx )= w l x²/4- w x³/6 - w l³/24

EIy =   wl x³/12 - w x⁴/24 - (w l ³/24 )x

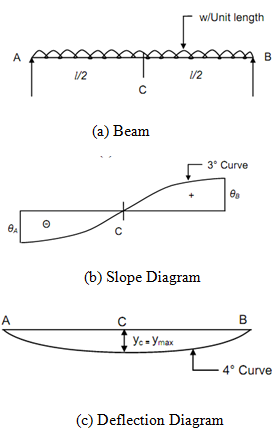
Slope at A, x = 0

(dx/dy)_A == θ_A = - w l³/ 24EI

Slope at B, x = l /2

EI (dy/dx) _B = EI θ_B = w l ³/4 -wl ³/6 -wl ³/24 =w l ²/24

∴          θ_B = + w l ³ / 24 EI

 Because of symmetry, the maximum deflection occurs at mid-span, i.e. at C,( x =l/2)  .

From Eq. (33),

EIy_max  = wl ⁴/  96 - wl ⁴/(24 × 16 )- wl ⁴ / (24 × 2)

= (wl⁴/384)  [4 - 1 - 8] = -( 5 /384)wl ⁴

∴          y max  =  - (5/384) (wl ⁴/ EI)

Figure