SS Beams with Triangular Load:

Figure illustrates a simply supported beam with distributed load which uniformly increases from 0 at A (x = 0) to w/unit length at B (x = l). Therefore, to load diagram appears as a triangle. Actually the total load = area of the triangle = (½) wl and at any section X-X at a distance x from A the rate of loading shall be  wx/ l , so that the load of shaded triangle = (1 /2)(wx/l) x = (1 /2)wx . This load will act at a distance of 2x/3  from  (centroid of triangles). The sum of the reactions (R_A + R_B) shall be equal to the load of entire triangle, that is

∑ y = 0

or,

R_A  + R_B = (½) × l × w = (wl/2)

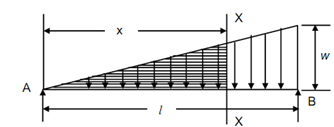
              SS Beam with Triangular Load

Taking moments around A,

wl /2× 2l/3 = R _B   × l

R _B   = wl/3 (↑)           ----------- (38)

From Eqs. (9.37) and (9.38),

R _A   = w l /6 (↑)                          ------------ (39)

Let a section X-X at distance x from A,

Intensity of load = (wl /x)

M = R A  x - (½) (wl/x) . x . (x/3)

            = wl x/6 - w x³/6l

The governing equation for deflection is following

EI (d ² y/ dx²)  = M =  wl x/6  - w x³/6l

Integrating the Eq. (41), we can obtain

EI (dy/ dx)      = w l x²/12 - w x⁴ /24l + C₁

EIy = wl x³ /36- w x⁵/120l + C₁ x + C₂

 The constants C₁ & C₂ may be found from the boundary conditions. The boundary conditions are following :

 at A,           x = 0,            y = 0

at B,             x = l,             y = 0

 Applying the BC (1) to the Equation (43), we can obtain C₂ = 0.

Applying the BC (2),

0 = wl ⁴ /36- w l ⁴ /120 + C₁ l 

C1 = (wl ⁴ /360 l )[3 - 10] = - 7 wl3/ 360

The slope & deflection equation shall be :

EI (dy /dx)= w l x ² /12-w x⁴ /24l - (7 /360)w l ³

EIy = wl x³/36-w x⁵/120 l- (7/360) w l ³ x

Slope at A, (x = 0)

            ( dy/dx) _A= θ_A =- 7 w l³/360 EI

Slope at B, (x = l)

EI (dy/dx) _B= EI θ_B  = w l³ /12- w l³  /24 -   (7 /360 )w l ³

=          wl ³/360 [30 - 15 - 7] = wl ³/45

∴          θ _B =    wl³/ 45 EI

Slope at mid-span, (x = l/2)  .

EI (dy/dx) = EI θ_C      = wl³ /48   -    wl ³ / (24 × 16) -   (7/360)   w l ³

= (wl³/24 × 16 × 15 )[30 - 15 - 7 × 16] = -67 wl ³/   5760

∴          θ_C        = -67 wl ³/5760EI

Deflection at centre, (x = l /2) .

EI y     =  (wl⁴ /(36 × 8) ) -(w l⁴/(12 × 32)       - (7 /360 × 2)w l ⁴

= (wl ⁴/630 × 32) [40 - 3 - 7 × 16] = - 71w l ⁴  /11520

 For maximum deflection,

dy / dx = 0

From Eq. (42),

0 = wl x² /12 -            w x⁴ /24 l -      (7/360) wl³

⇒         0 = 30 l ² x²  - 15 x⁴  - 7 l ⁴

⇒ x⁴  - 2 l 2 x²  +  7/15

∴  x = 0.5193l

From Eq. (43),

EI y_max  = wl /36 (0.5193l ) ³- w/120 l - (0.5193l )⁵

              -(7/360 × 2 )wl ³ (0.5193l )

= (wl ⁴ /360)    [14 - 0.11 - 3.64] = wl ⁴ / 153

∴          y_max  =- wl ⁴  /154

(a) Beam

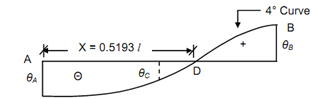
(b) Slope Diagram

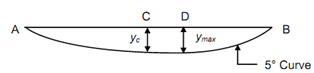
 (c) Deflection Diagram

Figure