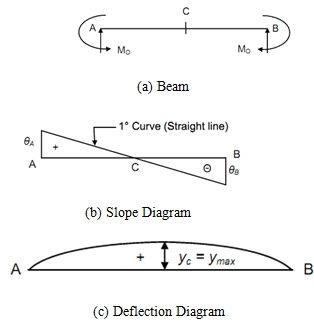
SS Beams with Equal End Couples:

∑ F_y  = 0 so that R_A  + R_B  = 0

Taking moments around A,

M ₀  - M ₀  = R_B  × l  ∴ R_B  = 0

From Eqs. (9.79) and (9.80),

R_A  = 0

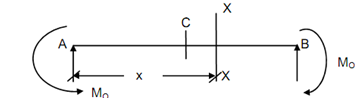
Figure: SS Beam with Equal End Couples

Let a section X-X at a distance x from A,

M  =- M ₀

The governing equation for deflection is

EI (d ² y / dx²) = M = - M ₀

 Integrating the Eq. (82), we can get

EI (dy/ dx) =- M ₀ x + C₁

EI (dy /dx)=- M ₀ x ² /2+ C₁ x + C₂

The constants C₁ & C₂ may be found from the boundary conditions. The boundary conditions are following:

 at A, x = 0, y = 0                 ----------- (1)

at B, x = l,  y = 0                     ------------ (2)

Applying the BC (1) to the Equation,

       C₂  = 0

Applying the BC (2) to the Equation,

0 =- M 0 l²  /2+ C _ll                  ∴ C  = M ₀ l /2

The slope and deflection equations shall be :

EI dy/ dx =- M₀  x + M ₀ l /2

EIy =- M ₀ x²/2 + (M ₀ l /2) x

Slope at A, (x = 0)

θ_A = + M ₀ l / 2 EI

Slope at B, (x = l)

EI θ _B  = - M 0 l + M ₀ l /2= - M ₀ l/2

∴ θ _B  = - M ₀ l/2 EI

Slope at C, (x = l /2) ,

EI θ _C  = - M ₀ l/2 + M ₀ l/2

∴          θ_C  = 0

Deflection at C, (x = l/2) ,

EIy =- (M 0/2)  ( l/2)²  + (M ₀ l/2) (  l/2)  + M₀  l ² /8

∴          y_C        =+ M 0 l²/8EI