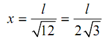SS Beams with a Couple:

A simply supported beam AB of span l upon which a couple of moment M₀ acts at C is illustrated in Figure

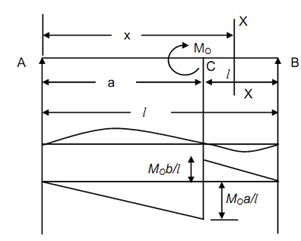
Figure

As sum of all forces in y direction is equal to zero,

                  R_A  + R_B  = 0  -----------(1)

Taking moments about A,

M ₀  = R_B  × l

R_B  =   M ₀/ l  (↑)           ------- (2)               

From Eqs. (1) & (2), 

R _A   =-   M ₀/ l (↓)

Let a section X-X at a distance x from A & write expression for BM at X-X. At this point you should note two significant features of expression for BM at X-X. If X-X lies among A & C, that means 0 < x ≤ a the BM is only because of R_A. If X-X is among C and B, that means a < x < b, then BM is because of R_A and M₀. So we write the second BM because the first is included but take care that M₀ is not let if integration is in the region 0 < x ≤ a and x is taken as (x - a) if integration is in the region a < x ≤ l and x = l. Therefore, in two cases we might apply BC at x = 0 & x = l. For particular presentation in the expression for M, M0 is placed in < > meaning that < M₀ > to be ignored in 0 < x ≤ a & to be let in a < x ≤ b with x replaced by (x - a). The process is known as Macaulays method

M  = R_A x + < M ₀ >

=- M ₀ x/ l + < M₀ >

 The governing equation for deflection is :

EI (d² y /dx²) = M = - M ₀ x/l + < M₀ >

Integrating the Eq. (9.55), we can get

EI  dy/ dx   =-  M 0 x² /2l + < M ₀ > [ x - a] + C₁

EIy =- M 0 x³ /6l +< M ₀ /2>  [x - a] ² + C₁ x + C₂

The constants of integration C₁ and C₂ may be found from the boundary conditions.

The boundary conditions are following:

 at A, x = 0, y = 0                         ------------- (1)

at B, x = l,   y = 0                         --------- (2)

Applying the boundary condition (1) to the Equation , with M₀ ignored, C₂ = 0.

Applying the BC (2) into the Equation (57),

0 =- M 0 l ² /6 + M 0/2 (l - a)² + C₁ l

C₁ =     M ₀ l /6 + (M ₀/2 l) (l - a)²

The slope & deflection equation shall be:

EI dy/ dx         =- M ₀ x²/2 l + < M ₀ > [x - a] + M ₀ l /6 - M ₀/2 l (l - a)²

EIy =- M ₀ x   + <M ₀/2>    [ x - a]²  + (M ₀ l/6) x - (M ₀/2 l) (l - a)²  x

If the moment M₀ is applied at the centre,

a = l /2

C  = M ₀ l /6 - M ₀ /2l ( l - l /2)² = ( M ₀ l/6) - (M ₀ l /8)= M ₀ l/24

The slope and deflection equation shall be :

EI (dy/dx) =- (M 0 x ² )/2l     + M₀ ( x - l /2)  + M ₀ l/24

EIy =- M ₀ x³/6l + (M ₀ /2) ( x - l /2)²+ (M ₀ l/24) x

Slope at A, (x = 0)

θ _A = + ( M ₀ l/24 EI)

Slope at B, (x = l)

EI θ _B = - M ₀ l/2 + M ₀ l/2 + M ₀ l/24 = M ₀ l/24

θ_B = M ₀ l /24 EI

Slope at C (x = l/2)  ,

EI θ_C   = - M ₀ l/8 + M ₀ l/24 = - M ₀ l/12

∴          θ_C = - M ₀ l /12 EI

Deflection at C ( x = l/2)  , y = 0

To get new slope,

+ M ₀ x/2 l = M ₀ l /24