Deflections of Simply Supported Beams (SS BEAMS):

Simply supported beam is supported on one hinged support & other roller support. The loads might be point loads or concentrated or distributed. Distributed loads might be uniformly distributed or distributed in any other manner. Triangular distribution is common, Udl, triangular loads, etc.

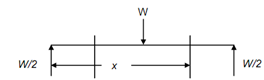
SS Beams with Central Point Load

AC = CB = l /2

Because of symmetry,

R _A   = R _B  = W / 2

Boundary conditions are known values of deflection & slope at particular values of

x. The Boundary Condition (BC) for this problem are :

(a) At x = 0, y = 0.

(b) At x = l, y = 0

(c) At x = l/2, dy/ dx = 0

Figure

Consider a section X-X at a distance x from A,

M = R _{A x} - W ( x -( l /2)

= (W/2)  x - W (x - l /2)

The governing equation for deflection is :

EI (d ² y/ dx² )  = M

or         EI (d ² y/ dx²) = (W/2)x - W ( x - ½) 2 < x < l

Consider a section X-X at a distance x from A,

M = R_A  x - W (x -( l/2)

= (W/2)  x - W ( x - (l/2)

The governing equation for deflection is :

EI ( d 2 y/ dx2 ) = M

or         EI(d 2 y/ dx2)

= (W/2) x - W ( x -(l/ 2 ))   (2 < x < l )

Integrating the above equation, we might obtain

EI( dy/ dx)      =( W/2)(  x2/2) -( W/ 2) - (x - (1/2))² + C1

C₁ is constant for integration.

Apply B.C 3, that is at

x = l /2 , dy/dx = 0

0 = (W /2)(l ² /8) + C₁

C₁ = - W l ² /16

 Integrating the above equation, we might get

EIy =   (W/4)( x3/3) - ((w/6)(x-(1/2))³ + C₁ x + C₂

∴          EIy =(w/4)( x3 /4)-( W  /6)  (x-(1/2))³ -Wl²x/16 + C2

with B.C 2, y = 0 at x = l

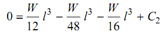
0 = (W/12) l³  - (W/48) l³  - (W/16) l ³  + C₂

or         C₂ = 0

Here is the constant of integration.

Applying the boundary condition (2) to the Eq. (10). By applying the BC (2) to the Eq., we will get

0 = (W/4)( l ²/ 4) + C₁ 

C₁ =- W l ² / 16

∴ The slope and deflection shall be :

EI(dy/dx) = W x²/4-( W/2)(x-(1/2))² - W l ²/16 (1/2) < x < l )

EIy = W x3     /12 -(w/6)(x-(1/2))³- W l ²/16