Deflection of Cantilever Beams:

Cantilever beams are fixed at one end and the other end is free. Since the x-axis is taken from left to right, the free end is taken at the left for convenience.

Cantilever Beams along Single Concentrated Load at Free End

Consider a cantilever beam loaded with a point load 'W' at free end. Consider a section X-X at a distance x from left end.

                      M = - W . x           (Hogging BM)

 The governing equation for deflection is following

EI = d ² y / dx² = M = - W x

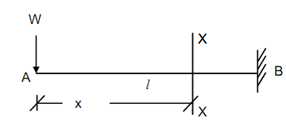
Figure

Integrating the Eq. (93), we might get

EI( dy/ dx) = - W x² /2 + C₁

EIy =- W x³ / 6   + C₁ x + C₂

The constants C₁ and C₂ can be found from the boundary conditions. The boundary conditions are following :

At B,             x = l,   dy/ dx      = 0 (Fixed end) ------------ (1)

At B,                 x = l,      y = 0                  -------- (2)

Applying the BC (1) into the Eq. (94), we might get

0 = - W l ₂ /2   + C₁

∴          C₁  =+  W l ₂ /2

 Applying BC (2) into the Eq. (95), we might  get

0 = - W l ₃ /6+ W l ₂ /2 × l + C₂

C₂  =- W l ₃ /3

The slope and deflection equations shall be :

EI (dy/dx)  = - Wl² /2 +wl²/2

EIy= Wx³ /6 + Wl²x/2 - Wl³/3

The maximum slope occurs at x = 0.

Slope at free end,

 θ _A  = + W l ²/ 2 EI

The maximum deflection occurs at x = 0.

y_max  =- W l ³ / 3 EI

Slope at centre ( x = l/2) ,

EI θ_C = -  W/2(1/2)₂ + (Wl₂/2)

θ_A = +3W l ²/8 EI

Deflection at centre (x = l/2)  ,

EIy_C  =- (w/6)(1/2)³ + W l ²/2´ (l/2)-  W l ³ /3

=- (W l ³ /48 )[- 1 + 12 - 16] =  - 5 W l³/48

 ∴         y_C    =- 5 W l₃/48 EI