Surface equation:

Plugging these new points back into the surface equation we have the following

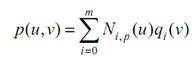
Thus, p (u ,v) is a point on the B-spline curve described by

 q₀ (v), q₁ (v), . . . , q_m (v). As a consequence, to determine p(u, v), what we need to do is to determine the point on this curve that corresponds to u. Therefore, de Boor's algorithm may be utilized again for this purpose.

Consider u be in knot span [u_c, u_{c + 1}). From the local modification property, only p + 1 control points shall participate the computation, where p is equal to the degree of the B-spline curve. Therefore, if u is not equal to u_c, the involved points are q_c (v), q_{c - 1}(v), . . . , q_{c - p}(v). Or else, if u is equal to u_c, a knot of multiplicity s, the involved points are q_{c - s} (v), q_{c - s - 1} (v), . . . , q_{c - p} (v). Based on this observation, even though each row of control points may produce a q_i (v), not all of them are required. Actually, only p + 1 rows are needed.

In summary, given u in [u_c, u_{c + 1}) and v in [v_d, v_{d + 1}), p (u, v), for row i in the range of c-p and c-s, by applying de Boor's algorithm to control points p_{i,d - q,} p_{i,d - q + 1}, . . . , p_{i, d - t} yields a new point q_i (v). Afterwards, by apply de Boor's algorithm to q_{c - p} (v), q_{c - p + 1} (v), . . . , q_{c -} s (v) and the result is p (u ,v)!