Series Resistance:
The total resistance within a series circuit is equivalent to the sum of all the parts of that circuit, as shown in equation (2-3).
RT = R1 + R2 + R3 ... etc. (2-3)
where
RT = resistance total
R1, R2, and R3 = resistance in series
Example: A series circuit has a 60, a 10, and a 150 resistor in series. What is the overall resistance of the circuit?
Solution:
RT = R1 + R2 + R3
= 60 + 100 + 150
= 310
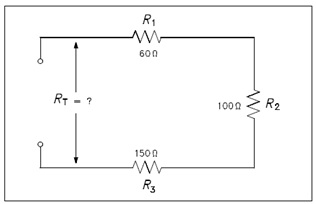
Figure: Resistance in a Series Circuit
The total voltage across a series circuit is equivalent to the sum of the voltages across every resistor in the circuit that was shown in the Figure as display in equation (2-4).
VT = V1 + V2 + V3 ... etc (2-4)
Where
VT = total voltage
V1= voltage across R1
V2= voltage across R2
V3= voltage across R3
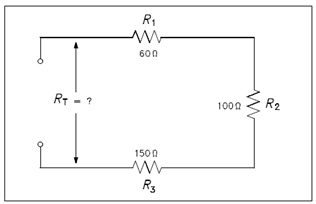
Figure: Voltage Drops in a Series Circuit
Ohm's law may now be applied to the entire series circuit or to individual component parts of the circuit. When used on individual component elements, the voltage across which part is equivalent to the current times the resistance of that part. For the circuit display in Figure, the voltage could be determined as display below.
V1 = IR1
V2 = IR2
V3 = IR3
VT = V1 + V2 + V3
VT = 10 volts + 24 volts + 36 volts
VT = 70 volts
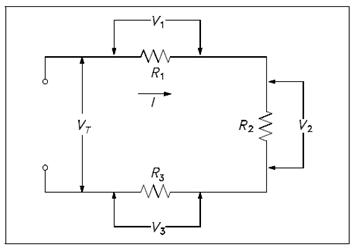
Figure: Voltage Total in a Series Circuit
To search the total voltage across a series circuit, multiply the current through the total resistance as display in equation (2-5).
VT = IRT (2-5)
where
VT = total voltage
I = current
RT = total resistance