Loop Equations:
As we have already known, Kirchhoff's Laws gives a practical means to solve for unknowns in a circuit. Kirchhoff's current law states which at any junction point in a circuit and the current arriving is equal to the current leaving. Within a series circuit the current is the similar at all points in that circuit. With parallel circuits, the total current is equal to the sum of the currents in every branch. Kirchhoff's voltage law states that the sum of all potential differences in a closed loop equals zero.
By using Kirchhoff's laws, it is possible to take a circuit with two loops and several power sources that are display in below figure and determine loop equations, solve loop currents, and solve individual element currents.
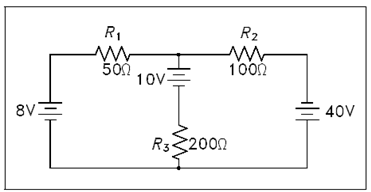
Figure: Example Circuit for Loop Equations
The 1st step is to draw an assumed direction of current flow (Figure 38). It does not matter whether the direction is correct. The resulting value for current will be negative if it is wrong.
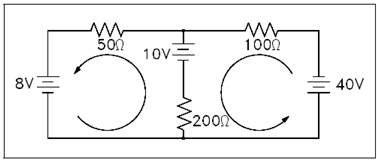
Figure: Assumed Direction of Current Flow
2nd, mark the polarity of voltage across every component in the Figure. It is necessary to select a direction for current by the center leg, other than it is not must to put in a new variable. It is simply I2 - I1.
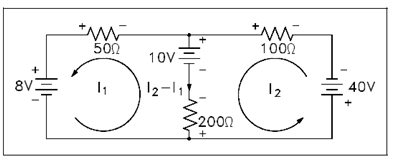
Figure: Marking Polarity
3rd, apply Kirchhoff's voltage law to loops one and two through picking a point in each loop and writing a loop equation of the voltage drops around the loop; then set the equation equal to zero.
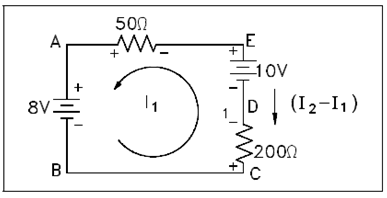
Figure: Applying Voltage Law to Loop 1
Figure 40 shows Loop one.
There is a raise in voltage of 8 volts From Point A to Point B. There is an increase in voltage of 200 (I2 - I1) From Point C to Point D. There is a decrease in voltage of 10 volts from Point D to Point E. There is a voltage decrease of 50I1 volts To Point E to Point A. The result in equation form is described in equation (2-16).
8 + 200 (I2 - I1) - 50 I1 - 10 = 0 (2-17)
Using the similar procedure for Loop 2 of Figure, the resulting equation is displays in equation (2-18).
10 - 200 (I2 - I1) + 40 - 100 I2 = 0 (2-18)
4th solve equations (2-17) and (2-18) concurrently. First, rearrange and combine like terms in the equation for Loop 1.
-50 I1 + 200 I2 - 200 I1 = 10 - 8
-250 I1 + 200 I2 = 2
Divide both sides by two.
-125 I1 + 100 I2 = 1
Combine and Rearrange like terms in the Loop 2 equation.
- 200 I2 + 200 I1- 100 I2 = -10 - 40
200 I1- 300 I2 = -50
Multiplying the Loop 1 equation through 3, and add it to the Loop 2 equation.
3(-125 I1 + 100 I2 =1) = -375 I1 +300I2 = 3
+200 I2 - 300I2 =50
-----------------------------------------------------------------
-175 I1 = -47
Solving for I1:
-175 I1 = -47
I1 = -47/-175= 0.2686 amp 268.6 mA
Solving for I2 using the Loop 1 equation:
-125 I1 + 100 I2 = 1
100 I2 = 1+ 33.58
I I2 = 34.58/100
I2 = 0.3458 amp = 345.8 mA
The current flow through R1 (50?) is I1. The current flow through R2 (100 ?) is I2, and through R3 (200?) is I2 - I1:
I3 = I2 - I1 345.8 mA - 268.6 mA
I3 = I2 - I1 77.2 mA
5th, apply Ohm's Law to acquire the voltage drops across Resistors R1, R2, and R3:
V1 = I1R1 = (0.2686 amps) (50 ?) = 13.43 Volts
V2 = I2R2 = (0.3458 amps) (100 ?) = 34.58 Volts
V3 = (I2 - I1) R3 = (0.0772 amps) (200?) = 15.44 Volts
6th check the calculations through applying Kirchhoff's Laws:
Check 1: Apply voltage law of kirchhoff to larger outer loop in the diagram.
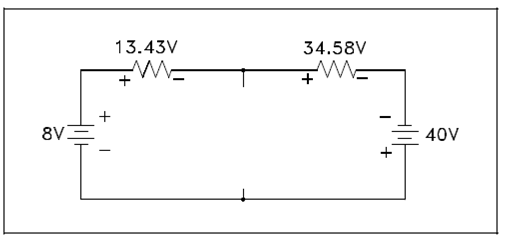
Figure: Applying Voltage Laws to Outer Loop
The sum of the voltage drops around the loop is essentially zero. (It is Not accurately zero due to rounding off.)
8- 13.43 - 34.58 + 40 = 0
0.01= 0
Thus, the solution checks.
Check 2: After that use Kirchhoff's current law at one of the junctions that was display in above figure.
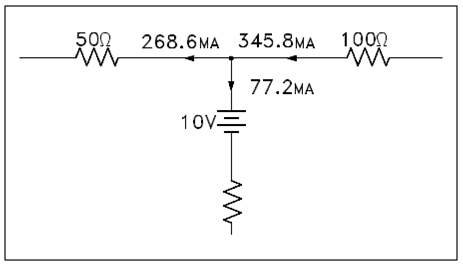
Figure: Applying Current Law to Junction
The total sum of the currents out of the junction is as follows:
0.2686 + 0.0772 = 0.3458 a
= 345.8 ma
The current into the junction is 345.8 ma.
The current into the junction is equal to the current out of the junction. Thus, the solution checks.