Possible cases:

The nature of this solution based on the term in the square root. There are three following possible cases:

(1)    (c/m) ²  > 4   (k /m) -  Overdamped case

(2)    (c/m)²  = 4 (k/m)   -  Critically damped case

(3)   (c/m)²  < 4 (k/m)   - Underdamped case

Let the critical damping coefficient be C_c, Hence,

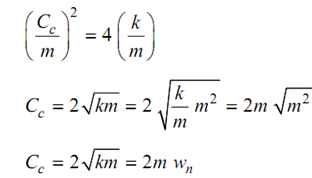
Almost all of the systems are underdamped.

Here,

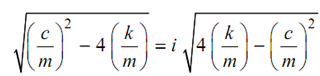
The ratio of damping coefficient (c) to critical damping coefficient is known as damping factor 'J'.

                                                J =  C /C_c                                               . . . (17)

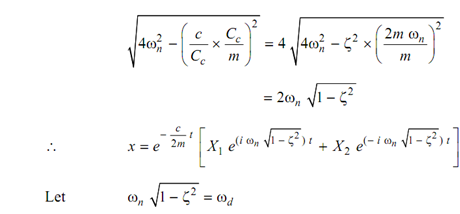.....(18)

here ω_d is natural frequency of the damped free vibrations.

Hence, underdamped case

x = e ^{-  (c /2m)} ( X₁  e^{i ωd t}  + X   e^{- i ωd t} )                      . . . (19)

For critically damped system

x = ( X₁ + X ₂ t ) e ^{- (  c/2m)   t}

For overdamped system

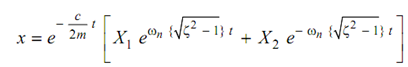      . . . (20)

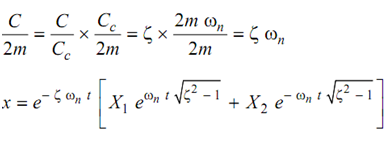                 . . . (21)

Figure

The Equation (19) may also be written as

x = X e^{-ζ ω}_n ^t cos (ω_d t + φ)                     . . . (23)

Here X and φ are constants. X represents amplitude and φ phase angle.

Assume at t = t,  x = x₀.

∴          x0  = X e^{- ζ ω}_n  ^t  cos (ω_d t + φ)                            . . . (24)

 After one time period

t = t + t _p             and            x = x₁

∴          x  = X e^{- ζ ω}_n ^{(t + t p )}  cos {ω_d (t + t_p ) + φ}                           . . (25)

Dividing Eq. (24) by Eq. (25)

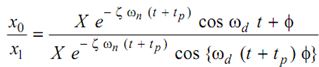
As

 t _p  = 1/  f _p = 2π/ ω_d

or         ω_d t _p  = 2π

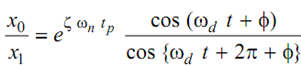
Since    cos θ= cos (2π+ θ)

∴          cos (ω_d  t + φ) = cos {ω_d  t + 2π + φ}

 ∴         x₀  /x₁ = e ^{ζ ωn t p}

 or        L  = x₀ /x₁= ζ ω_n t_p = ζ ω_n (2π/ ω_d )=

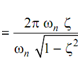
or

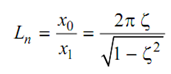                          -------- (26)

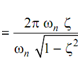 is known as logarithmic decrement.

If at  t = t + n t _p

It might be proved that

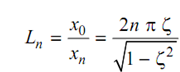         --------(27)

If         

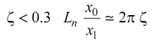
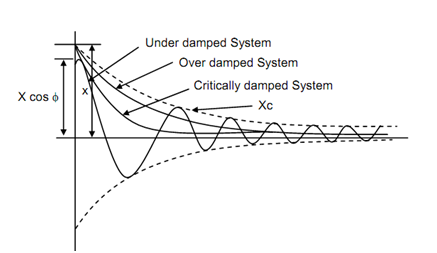
Figure 8 shows displacement time diagram for the above indicated three cases. For critically damped & overdamped system mass returns to its original place (indisplaced) gradually and there is no vibration. Vibration is possible just in the underdamped system as the roots of Eq. (14) are hard and solution consists of periodic functions (Eq. (22)).