Free Torsional Vibration of a Single Rotor System:

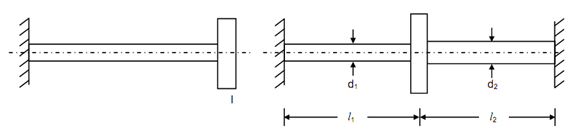
In torsional vibration, all of the particles of the system vibrate along with circular arcs with their centers with the axis of rotation. Figure 10 mentions single rotor systems. In both of the cases (i) and (ii), there is one inertia 'I' only.

(i)                                                                    (ii)

          Figure 10

In part (i) this is supported by one shaft segment and in part (ii) this is supported by the two shaft segments.

The differential equation for the rotor illustrated in Figure 10(i) there are two couples, that is torsional elastic and inertia couple. If inertia is slightly twisted say by angle 'θ', the couple is specified by

                                                                 (k_t  θ)

here k_t is torsional stiffness that is given through following equation

            k_t  = T/ θ = G J /l

here G is modulus of rigidity,

J is polar moment of inertia, and

l is length of shaft.

The differential equation for the rotor specified in Figure 10(i) is

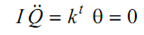              ------------ (32)

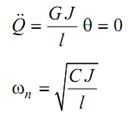                   ----------------(33)

For the shaft illustrated in Figure (b), the two segments are acting as parallel springs. Hence, the differential equation for this will be

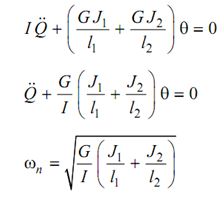     -----------(34)