Mathematical Representation of Curvilinear Motion:

Let t^′ and n^′ make an angle Δ φ along with their old directions. Now we extend the unit normal vectors n^ and n^ and let them meet at C which is called as the centre of curvature and length CP = ρ is called the radius of curvature.

∴ Δ s = ρ . Δ φ

Δ s / Δ t = ρ Δ φ/ Δ t

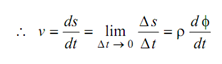
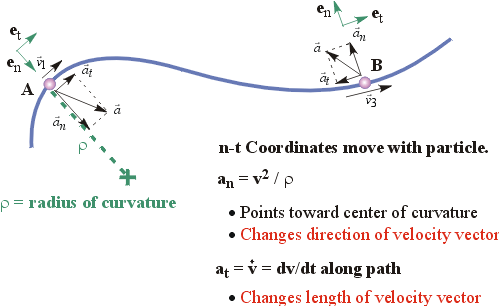
The velocity at point P′ shall be different from velocity at P and may be written as v + Δ v . The change in velocity Δ v shall be a vector and shall be caused by an increase in the magnitude plus a change in the direction of vector V at P as illustrated in Figure

v + Δ v = (v + Δ v) t ′(Vectorially)

so, acceleration a shall be

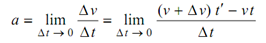
As        Δ t → 0,         P′ → P

 Resolving along tangent and normal at P.

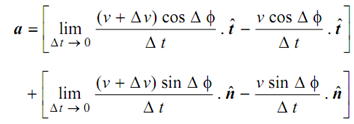
but as Δ t → 0, Δ φ → 0 and lim sin φ = φ and lim cos φ = 1.

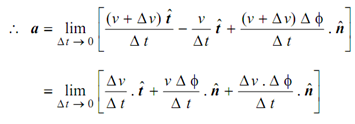
Δ v . Δ φ is the product of two small quantities, therefore we neglect it. Also we have

Δ φ = Δ s /ρ     and      Δ s / Δ t = v

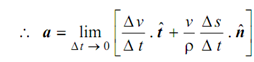
= dv /dt . t^ + (v ² / ρ ). n^

If a_t = tangential component of acceleration, and a_n = normal component of acceleration.

 Then

a = a_t t^+ a_n n^

= dv/ dt . t^ + (v²/ ρ) . n^

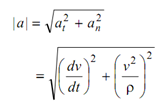
This resultant acceleration shall make an angle β with the normal to the curve at P.

Then                   tan β = a_t / a_n ,

Here, we should remember that normal acceleration is oriented towards the centre of curvature C.

 In case of rectilinear motion ρ = ∞ and an = 0. The acceleration a = at  = dv / dt and shall be always along the path of the particle. If equation of the path of the particle is specified by

y =  f ( x) , then the radius of curvature at a point whose coordinates are x and y is given

by

1/ ρ = ±  (d ² y/ d x ²) / [1+ (dy/dx)²] ^(3/2)